【BZOJ 1177】 [Apio2009]Oil

【链接】 我是链接,点我呀:)

【题意】

在这里输入题意

【题解】

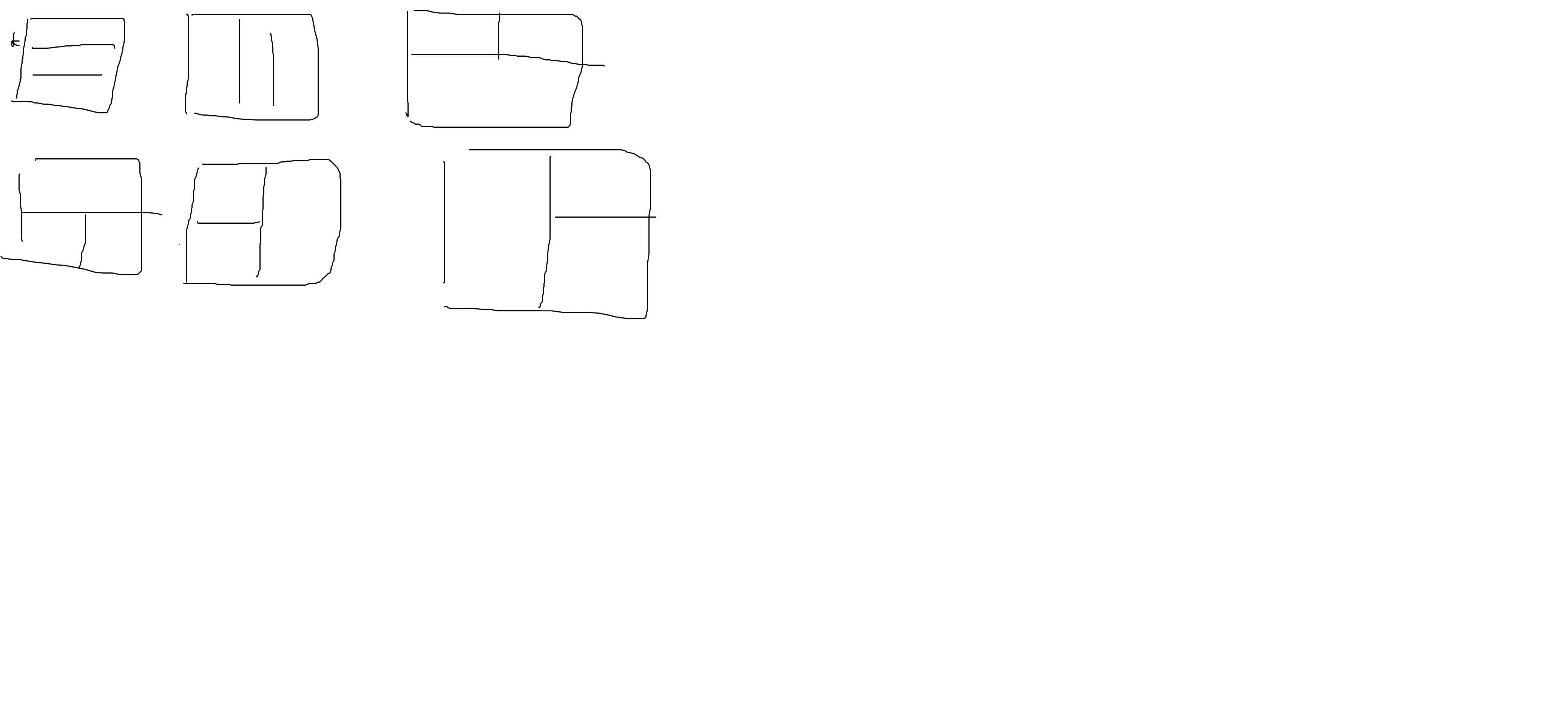
如上图。
显然如果三个正方形。只可能是上面的情况。
则可以处理一下左上角、右上角、左下角、右下角的前缀最大正方形(dp),以及以某一列为底部,某一行为底部的最大正方形和。
然后枚举一下两条分界线就能做出来啦。
细节题。

【代码】

#include <bits/stdc++.h>
#define LL long long
#define rep1(i,a,b) for (int i = a;i <= b;i++)
#define rep2(i,a,b) for (int i = a;i >= b;i--)
#define all(x) x.begin(),x.end()
#define pb push_back
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
using namespace std;

const double pi = acos(-1);
const int dx[4] = {0,0,1,-1};
const int dy[4] = {1,-1,0,0};
const int N = 1500;

int n,m,k;
int x[N+10][N+10],a[N+10][N+10],b[N+10][N+10],c[N+10][N+10],d[N+10][N+10],maxh[N+10],maxl[N+10],A[N+10][N+10];

int calc(int x,int y){
    return A[x][y]-A[x-k][y]-A[x][y-k]+A[x-k][y-k];
}

int main(){
	#ifdef LOCAL_DEFINE
	    freopen("rush_in.txt", "r", stdin);
	#endif
    scanf("%d%d%d",&n,&m,&k);
    rep1(i,1,n)
        rep1(j,1,m)
            scanf("%d",&x[i][j]);

    rep1(i,1,n)
        rep1(j,1,m)
            a[i][j]=x[i][j] + a[i-1][j]+a[i][j-1]-a[i-1][j-1];

    rep1(i,1,n)
        rep1(j,1,m)
            A[i][j] = a[i][j];
    memset(a,0,sizeof a);

    rep1(i,k,n)
        rep1(j,k,m)
            maxh[i] = max(maxh[i],calc(i,j));

    rep1(j,k,m)
        rep1(i,k,n)
            maxl[j] = max(maxl[j],calc(i,j));

    rep1(i,k,n)
        rep1(j,k,m){
            a[i][j] = max(max(a[i-1][j],a[i][j-1]),calc(i,j));
        }

    rep1(i,k,n)
        rep2(j,m-k+1,1)
            b[i][j] = max(max(b[i-1][j],b[i][j+1]),calc(i,j+k-1));

    rep2(i,n-k+1,1)
        rep1(j,k,m){
            c[i][j] = max(max(c[i+1][j],c[i][j-1]),calc(i+k-1,j));
        }
    rep2(i,n-k+1,1)
        rep2(j,m-k+1,1)
            d[i][j] = max(max(d[i+1][j],d[i][j+1]),calc(i+k-1,j+k-1));

    int ans = 0;
    rep1(i,k,n)
        rep1(j,i+k,n){
            if (j+k>n) continue;
            ans = max(ans,a[i][m]+maxh[j]+c[j+1][m]);
        }

    rep1(i,k,m)
        rep1(j,i+k,m){
            if (j+k>m) continue;
            ans = max(ans,a[n][i]+maxl[j]+d[1][j+1]);
        }

    rep1(i,k,n-k+1)
        rep1(j,k,m-k+1){
            ans = max(ans,a[i][j]+b[i][j+1]+c[i+1][m]);
            ans = max(ans,a[i][m]+c[i+1][j]+d[i+1][j+1]);
            ans = max(ans,a[i][j]+b[n][j+1]+c[i+1][j]);
            ans = max(ans,a[n][j]+b[i][j+1]+d[i+1][j+1]);
        }

    printf("%d\n",ans);
	return 0;
}