最小生成树（MST，minimum spanning tree）

生成树：由图生成的树，由图转化为树，进一步可用对树的相关操作来对图进行操作。最小指的是权值最小；

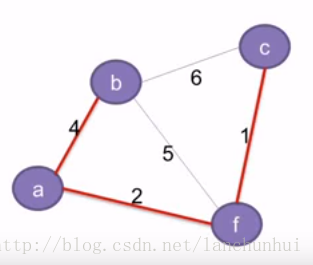
• 生成树是边的集合，如下图所示的最小生成树：MST={{a,b},{a,f},{f,c}}

  

本文主要探讨带权无向连通图（网络）上的最小生成树问题，以及求最小生成树的两个算法。

0. 生成数

• n 个顶点的图，有 n−1 棵生成树；

1. 最小生成树

最小生成树有很多实际应用。例如，将网络顶点看做城市，边看做连接城市的通信网，边的权看做连接城市的通信线路的成本，根据最小生成树建立的通信网就是这些城市之间成本最低的通信网。

2. Kruskal 算法

3. Prim 算法

Prim 算法的设计出发点与 Kruskal 算法完全不同：

• Prim 算法从一个顶点出发，逐步扩充包含该顶点的部分生成树 T；

Prim 算法的实施，需要用到关于最小生成树的一个重要特性，描述如下：

设 G=(V,E) 是一个网络，U 是 V 的任一真子集，设 e=(u,v)∈E，且u∈U,v∈V−U（也就是说，e 的一个端点在 U 里，另一个不在），且 e 在 G 中所有一个端点在 U 而另一个端点在 V−U 的边中权值最小，那么 G 中必有一棵包含边 e 的最小生成树。