Day4下午解题报告

预计分数：30+30+0=60

实际分数：30+30+10=70

稳有个毛线用，，又拿不出成绩来，，

T1

https://www.luogu.org/problem/show?pid=T15626

一开始掉进了数列的坑里就傻乎乎的没出来过

样例给了个3 5 ，推着推着就感觉是斐波那契数列，GG

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<map>
 #include<ctime>
 #include<cstdlib>
 #define LL long long
 using namespace std;
 const LL MAXN=1e6;
 const LL INF=0x7ffff;
 inline LL read()
 {
     char c=getchar();LL flag=,x=;
     while(c<''||c>'')    {if(c=='-')    flag=-;c=getchar();}
     while(c>=''&&c<='')     x=x*+c-,c=getchar();return x*flag;
 }
 LL f[MAXN];
 LL ans=;
 map<LL,bool>vis;
 LL gcd(LL a,LL b)
 {
     return b==?a:gcd(b,a%b);
 }
 int main()
 {
 //    freopen("seq.in","r",stdin);
 //    freopen("seq.out","w",stdout);
     LL a=read(),b=read();
     if(a==b)
     {
         printf("");
         return ;
     }
     LL g=gcd(a,b);
     a/=g,b/=g;
     f[]=a,f[]=b;f[]=abs(b-a);vis[f[]]=;vis[f[]]=;
     LL tot=;
     bool flag=;
     LL t=clock();
     LL x=f[],y=f[],z;
     while(y!=)
     {
         if(clock()-t>=)
         {
             printf("-1");
             exit();
             break;
         }
         z=abs( x-y );
         if(vis[z]==)
             ans++,vis[z]=;
         x=y,y=z;
     }
     printf("%lld",ans);
     return ;
 }

正解：

更相减损术

用除法优化减法

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#define LL long long
using namespace std;
inline LL read()
{
	char c=getchar();LL flag=1,x=0;
	while(c<'0'||c>'9')	{if(c=='-')	flag=-1;c=getchar();}
	while(c>='0'&&c<='9')	x=x*10+c-48,c=getchar();return x*flag;
}
LL a,b;
LL ans=0;
int main()
{
	a=read();b=read();
	if(a<b)	swap(a,b);
	LL c=a%b;
	while(c)
	{
		ans+=a/b;
		a=b;b=c;c=a%b;
	}
	ans+=a/b;
	ans++;
	printf("%lld",ans);
	return 0;
}

　　

T2

https://www.luogu.org/problem/show?pid=T15627

mdzz裸地暴力一分都没有啊。。。

不过30分的貌似可以套最大生成树做。。

按说用最大生成树可以过50分的，但是我不会判断t。。GG

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<queue>
 #include<algorithm>
 using namespace std;
 const int MAXN=1e5;
 const int INF=0x7ffff;
 inline int read()
 {
     char c=getchar();int flag=,x=;
     while(c<''||c>'')    {if(c=='-')    flag=-;c=getchar();}
     while(c>=''&&c<='')     x=x*+c-,c=getchar();return x*flag;
 }
 struct node
 {
     int u,v,w,nxt;
 }edge[MAXN];
 int head[MAXN];
 int num=;

 inline void add_edge(int x,int y,int z)
 {
     edge[num].u=x;
     edge[num].v=y;
     edge[num].w=z;
     edge[num].nxt=head[x];
     head[x]=num++;
 }
 int t[MAXN];
 int vis[MAXN];

 struct node2
 {
     int u2,v2,w2,f2;
 }edge2[MAXN];
 int num2=;
 inline void add_edge2(int x2,int y2,int z2)
 {
     edge2[num2].u2=x2;
     edge2[num2].v2=y2;
     edge2[num2].w2=z2;
     num2++;
 }

 int bfs(int now,int val)
 {
     queue<int>q;q.push(now);
     int ans=;
     memset(vis,,sizeof(vis));vis[now]=;
     while(q.size()!=)
     {
         int p=q.front();q.pop();
         for(int i=head[p];i!=-;i=edge[i].nxt)
             if(vis[edge[i].v]==&&edge[i].w>=val)
                 vis[edge[i].v]=,q.push(edge[i].v),ans++;
     }
     return ans;
 }
 int fa[MAXN];
 int n,m;
 int comp(const node2 &a,const node2 &b)
 {
     return a.w2>b.w2;
 }
 int find(int x)
 {
     if(fa[x]==x)    return x;
     else return fa[x]=find(fa[x]);
 }
 inline void unionn(int x,int y)
 {
     fa[find(x)]=find(y);
 }
 void kruskal()
 {
     sort(edge2+,edge2+num2,comp);
     int tot=;
     for(int i=;i<=num2-;i++)
     {
         if(find(edge2[i].u2)!=find(edge2[i].v2))
         {
             unionn(edge2[i].u2,edge2[i].v2);
             add_edge(edge2[i].u2,edge2[i].v2,edge2[i].w2);
             add_edge(edge2[i].v2,edge2[i].u2,edge2[i].w2);
             tot++;
             if(tot==n-)    break;
         }
     }
 }
 int main()
 {
     //freopen("car.in","r",stdin);
 //    freopen("car.out","w",stdout);
     memset(head,-,sizeof(head));
     n=read(),m=read();
     for(int i=;i<=n;i++)
         fa[i]=i;
     if(n<=)
     {
         for(int i=;i<=m;i++)
         {
             int x=read(),y=read(),z=read();
             add_edge(x,y,z);
             add_edge(y,x,z);
         }
         for(int i=;i<=n;i++)// 枚举所有点
         {
             int now=,out=;
             while()
             {
                 int p=bfs(i,now);
                 if(p==)    break;
                 t[now++]=p;
             }
             for(int i=;i<=now-;i++)
                 out+=abs(t[i]-t[i+])*abs(t[i]-t[i+]);
             printf("%d ",out);
         }
     }
     else
     {
         for(int i=;i<=m;i++)
         {
             int x=read(),y=read(),z=read();
             add_edge2(x,y,z);
             add_edge2(y,x,z);
         }
         kruskal();
         for(int i=;i<=n;i++)// 枚举所有点
         {
             memset(t,,sizeof(t));
             int now=,out=;
             while()
             {
                 int p=bfs(i,now);
                 if(p==)    break;
                 t[now++]=p;
             }
             for(int i=;i<=now-;i++)
                 out+=abs(t[i]-t[i+])*abs(t[i]-t[i+]);
             printf("%d ",out);
         }
     }
     return ;
 }

 /*

 3 2
 1 2 1
 2 3 2

 4 5
 1 4 2
 1 2 3
 2 4 1
 2 3 4
 3 4 2

 */

暴力

正解

最大生成树

用并查集维护的时候，每次维护的时候在两个点上面新开一个节点

这样就形成了一颗二叉树

剩下的就不会了。。。

https://www.luogu.org/problem/show?pid=T15628

T3

https://www.luogu.org/problem/show?pid=T15628

一眼动态规划，

很好写，但是时间复杂度是O(n*m*k)GG,一分没有

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 using namespace std;
 const int MAXN=;
 const int INF=0x7ffff;
 inline int read()
 {
     char c=getchar();int flag=,x=;
     while(c<''||c>'')    {if(c=='-')    flag=-;c=getchar();}
     while(c>=''&&c<='')     x=x*+c-,c=getchar();return x*flag;
 }
 int dp[MAXN][MAXN];
 // 第i个数 已经选了j个 第i个一定选  最小值
 int a[MAXN];
 int main()
 {
 //    freopen("number.in","r",stdin);
 //    freopen("number.out","w",stdout);
     int n=read(),m=read(),need=read();
     memset(dp,0x3f,sizeof(dp));
     for(int i=;i<=n;i++)    a[i]=dp[i][]=read();
     for(int i=;i<=n;i++)
         for(int j=i-m;j>=;j--)
             for(int k=;k<=need;k++)
                 dp[i][k]=min(dp[i][k],dp[j][k-]+a[i]);
     int ans=INF;
     for(int i=;i<=n;i++)
         ans=min(ans,dp[i][need]);
     printf("%d",ans);
     return ;
 }
 /*
 6 2 3
 9 8 1 3 5 4 //14

 5 2 2
 4 7 1 1 1//2

 5 2 2
 4 3 44 44 1 //4

 7 3 1
 4 6 7 1 2 3 4// 1

 7 3 3
 4 6 7 1 2 3 4// 9

 */

mmp。。。。。

正解

我就不吐槽啥了

这**出题人压根就没给暴力分啊。

考虑如何在O(n)内算出不考虑k，只考虑m的最大值

很显然的一个结论

设f(x)为1-n中，长度为m的限制下，选x个数的图像的增长区线

那么f(x)会增长的越来越快

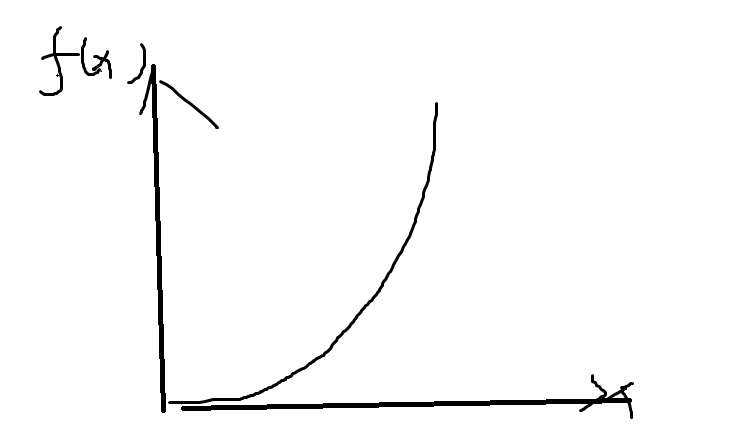
二分一个c，为(k-1,f(k-1) ) 与 (k,f(k) ) 的斜率

 

 #include<cstdio>
 #include<cstdlib>
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 typedef long long LL;
 const int N=;
 const LL inf=;
 int n,m,x,y,z,L,sum;
 int cnt[N];
 LL ans0,ans;
 LL f[N],s[N];
 LL read()
 {
     LL x=,f=;char ch=getchar();
     while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 void solve(LL c)
 {
     int i,a,tot=;
     LL ss=;
     memset(cnt,,sizeof(cnt));
     memset(f,,sizeof(f));
     for(i=;i<=n;i++)
     {
         a=i-m;
         if(a>=&&c-s[a]>&&(f[a]>ss||(f[a]==ss&&cnt[a]<tot)))
         {
             ss=f[a];
             tot=cnt[a];
         }
         if(c-s[i]>)
         {
             f[i]=ss+c-s[i];
             cnt[i]=tot+;
         }
     }
     ans0=sum=;
     for(i=;i<=n;i++)
         if(f[i]>ans0||(f[i]==ans0&&sum>cnt[i]))
         {
             sum=cnt[i];
             ans0=f[i];
         }
 //    printf("%d %lld %lld\n",sum,c,ans0);
 }
 int pd(LL c)
 {
     solve(c);
     if(sum<L) return ;
     else return ;
 }
 int main()
 {
     int a,b,c,i,j,k;
     LL l,r;
     freopen("number.in","r",stdin);
     freopen("number.out","w",stdout);
     n=read();
     m=read();
     L=read();
     for(i=;i<=n;i++)
         s[i]=read();
 //    for(i=1;i<=n;i++)
 //        if(i%m==1) ans+=(LL)s[i];
 //    printf("%lld\n",ans);
     ans=;
     l=;
     r=(LL)inf*N/;
     while(l<r-)
     {
         LL mid=(l+r)/;
         if(pd(mid)) l=mid;
         else r=mid;
     }
     if(pd(r))
     {
         solve(r);
         ans=(LL)L*r-ans0;
 //        printf("%d\n",sum);
     }
     else
     {
         solve(l);
         ans=(LL)L*l-ans0;
     }
     printf("%lld\n",ans);
 }
 /*
 6 5 2
 100 1 1 1 1 100
 */

STD

 总结

上午那场，出题人给了：50+80+0的暴力，我正好没做T2

下午这场，出题人给了：30+30+0的暴力，我正好做了T3

mmp..

摆明了把我这种纯暴力选手往死里坑啊，，，，

不过还好明天就不是这个出题人了，(* ￣︿￣)(* ￣︿￣)(* ￣︿￣)(* ￣︿￣)(* ￣︿￣)(* ￣︿￣)(* ￣︿￣)(* ￣︿￣)