CF47A Triangular numbers

CF47A Triangular numbers

题意翻译

给定一个数n，问你是否存在一个整数i，满足i*(i+1)/2=n。

若存在，输出"YES",否则输出"NO".

1<=n<=500

Translated by @稀神探女

题目描述

A triangular number is the number of dots in an equilateral triangle uniformly filled with dots. For example, three dots can be arranged in a triangle; thus three is a triangular number. The nn -th triangular number is the number of dots in a triangle with nndots on a side. 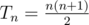. You can learn more about these numbers from Wikipedia (http://en.wikipedia.org/wiki/Triangular\_number).

Your task is to find out if a given integer is a triangular number.

输入输出格式

输入格式：

The first line contains the single number nn ( 1<=n<=5001<=n<=500 ) — the given integer.

输出格式：

If the given integer is a triangular number output YES, otherwise output NO.

输入输出样例

输入样例#1： 复制

1

输出样例#1： 复制

YES

输入样例#2： 复制

2

输出样例#2： 复制

NO

输入样例#3： 复制

3

输出样例#3： 复制

YES

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
int n;
int main(){
    scanf("%d",&n);
    for(int i=;i<=n;i++)
        if(i*i+i==*n){
            cout<<"YES";
            return ;
        }
    cout<<"NO";
}