[BZOJ 2395] Time is money

Link：

BZOJ 2395 传送门

Solution：

算是一类比较经典的模型：

即对于一类经典问题，每点由1个权值化为2个权值，最终求$sigma(val_1)*sigma(val_2)$

对于此题，

设每棵生成树为坐标系上的一个点，$sigma(x_i)$为横坐标，$sigma(y_i)$为纵坐标。

则问题转化为求一个点，使得$xy=k$最小。

即，使过这个点的反比例函数$y=k/x$最接近坐标轴

算法如下图：

（1）:求得分别距$x$轴和$y$轴最近的生成树（点）：$A$、$B$（分别按x权值和y权值做最小生成树即可）。

（2）寻找一个在$AB$的靠近原点一侧的且离$AB$最远的点$C$。

（3）递归地分别往$AC$、$BC$靠近原点的一侧找。递归边界：该侧没有点了。

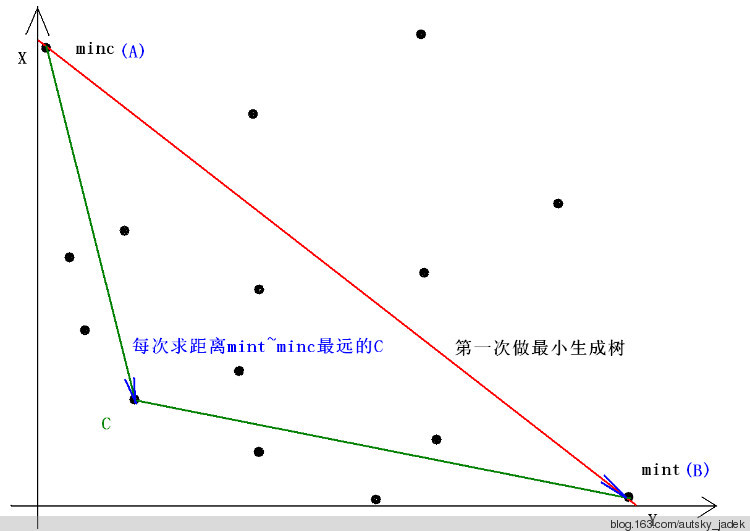
剩下来就是一些寻找$C$点实现细节了：

由于$C$离$AB$最远，所以$S\Delta ABC$面积最大。

因此最小化$\vec{AB} \times \vec{AC}$即可（此时叉积为负）

化简一下式子，将每个点的权值修改为 $y[i]*(Bx-Ax)+x[i]*(Ay-By)$ 做最小生成树，找到的是$C$。

Code：

//by NewErA
#include <bits/stdc++.h>

using namespace std;
typedef long long ll;

const int MAXN=205;
const int MAXM=1e4+5;
struct Vector
{
    int x,y;
    Vector(const int &A,const int &B){x=A;y=B;}Vector(){}
};
struct edge
{
    int to,from,c,t,w;
}e[MAXM];
bool cmp(edge x,edge y){return x.w<y.w;}
Vector operator - (const Vector &a,const Vector &b){return Vector(a.x-b.x,a.y-b.y);}
Vector operator + (const Vector &a,const Vector &b){return Vector(a.x+b.x,a.y+b.y);}
int Cross(const Vector &a,const Vector &b){return a.x*b.y-a.y*b.x;}

int n,m,f[MAXN],cnt=0;
Vector res=Vector(1e9,1e9),minc,mint;

int find(int x){return f[x]==x?x:f[x]=find(f[x]);}

Vector Kruscal()  //求解最小生成树
{
    for(int i=0;i<=n;i++) f[i]=i;
    Vector cur=Vector(0,0);cnt=0;

    for(int i=1;i<=m;i++)
    {
        int fx=find(e[i].from),fy=find(e[i].to);
        if(fx!=fy)
        {
            cnt++;f[fx]=fy;
            cur.x+=e[i].c;cur.y+=e[i].t;
            if(cnt==n-1) break;
        }
    }

    ll P1=(ll)res.x*res.y,P2=(ll)cur.x*cur.y; //记得开long long
    if(P1>P2 || (P1==P2 && res.x>cur.x))
        res=cur;
    return cur;
}

void Solve(Vector A,Vector B)
{
    for(int i=1;i<=m;i++)
        e[i].w=e[i].c*(A.y-B.y)+e[i].t*(B.x-A.x);  //将边权加以转化
    sort(e+1,e+m+1,cmp);
    Vector C=Kruscal();
    if(Cross(B-A,C-A)>=0) return;  //终止条件：叉积大于等于0
    Solve(A,C);Solve(C,B);
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
        scanf("%d%d%d%d",&e[i].from,&e[i].to,&e[i].c,&e[i].t);

    for(int i=1;i<=m;i++) e[i].w=e[i].c;
    sort(e+1,e+m+1,cmp);minc=Kruscal();

    for(int i=1;i<=m;i++) e[i].w=e[i].t;
    sort(e+1,e+m+1,cmp);mint=Kruscal();

    Solve(minc,mint);
    printf("%d %d",res.x,res.y);

    return 0;
}

Review：

这类模型一般很好识别，就当模板练了吧