C语言中函数调用过程(如何管理栈空间)

ps:先做草稿，以后有时间再整理并贴图，:)

主要是利用栈底寄存器(ebp)、栈顶寄存器(esp)跟eax寄存器(存储返回值)来实现。

假设P调用Q：

P()

{

　　Q(1,2);

}

(跟实际情况可能有点差异，主要还是用来了解函数调用的过程)

1.调用前准备，将Q的参数放到栈中(非push)

mov $1, (%esp)

mov $2, 4(%esp)

2.调用call 0x12345678 (Q的地址)

首先将函数的返回地址(call语句后的那条指令的地址)进栈，

然后跳到0x12345678执行Q的代码。

3.将旧的ebp进栈(用于退出Q时还原)

push %ebp

4.设置新的栈底

mov %esp, %ebp

5.为Q分配栈空间(栈是向下生长的)

sub $24, %esp    (16 * k + 8，用于对齐)

6.执行Q的相关代码。局部变量/参数是根据esp、ebp跟偏移量来进行存取的。

7.函数离开前将返回值赋值给%eax。

8.调用leave，相当于:

mov %ebp, %esp (还原栈顶)

pop %ebp (还原栈底)

9.处理返回值并接着P接着的代码继续执行。

贴多一张Linux运行时存储器映像的图

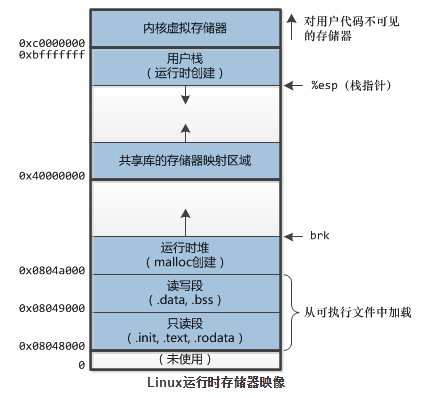
.text 　　代码段

.rodata   存储字符串常量

.data　　存储已初始化的全局/静态变量

.bss 　　 存储为初始化/初始化为0的全局/静态变量(在可执行文件中只占一个占位符，程序加载的时候才分配空间)

ELF文件中有.rel.text/.rel.data段，用于重定位。