【Foreign】Research Rover [DP]

Research Rover

Time Limit: 25 Sec  Memory Limit: 256 MB

Description

　　

Input

　　

Output

　　仅一行一个整数表示答案。

Sample Input

　　3 3 2 11
　　2 1
　　2 3

Sample Output

　　333333342

　　

HINT

　　

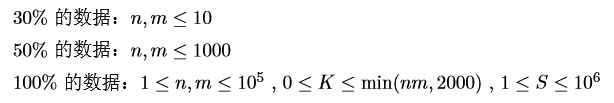
Main idea

　　从(1,1)走到(n,m)，每次可以向右或向下走一步，有K个特殊点，初始有一个权S，每经过一个特殊点S=(S+1)/2，询问到(n,m)的S的期望。

Solution

　　我们显然想到了DP，研究一下题目，发现可以按照到达目标之后S的值分类，显然S的取值只和经过特殊点的个数相关。并且由于每经过一个特殊点，S的值就会/2，那么显然只有log2(S)种取值，所以我们可以去考虑一个O(K^2log(S))的做法。

　　首先，从起点走到终点的总方案数是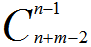：，我们可以将终点也当做特殊点，那么就可以令 f[i][j] 表示到了第 i 个目标点，经过 j 个目标点的方案数。

　　那么我们可以考虑容斥：。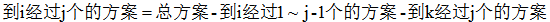

　　那么写成表达式也就是：

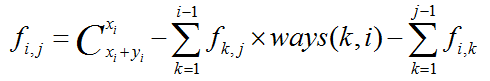
　　其中：，计算方法显然和计算总方案一样，运用组合数。（组合数计算的时候求一下乘法逆元和阶乘逆元即可）

　　这样的话就可以算出到终点经过 i 个特殊点的方案、乘上对应的S的值、然后计算一下、再乘上总方案的乘法逆元就是答案了。

　　效率就是O(k^2 * log(S))，就可以解决这道题啦。\(≧▽≦)/

Code

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef long long s64;
 const int ONE = ;
 const int INF = ;
 const int MOD = 1e9+;

 int Mod = MOD;
 int n,m,K,S;
 int f[ONE][];
 int Jc[ONE],inv[ONE];
 int A[],a_num;
 int Up;

 struct power
 {
         int x,y;
 }a[ONE];

 int cmp(const power &a,const power &b)
 {
         return a.x+a.y < b.x+b.y;
 }

 int get()
 {
         int res,Q=;    char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 namespace D
 {
         int Quickpow(int a,int b)
         {
             int res=;
             while(b)
             {
                 if(b&) res=(s64)res*a%MOD;
                 a=(s64)a*a%MOD;
                 b>>=;
             }
             return res;
         }

         void Deal_Jc(int k)
         {
             Jc[]=;
             for(int i=;i<=k;i++) Jc[i] = (s64)Jc[i-]*i%MOD;
         }

         void Deal_inv(int k)
         {
             inv[]=;    inv[k] = Quickpow(Jc[k],MOD-);
             for(int i=k-;i>=;i--) inv[i] = (s64)inv[i+]*(i+)%MOD;
         }

         void pre(int k)
         {
             Deal_Jc(k);    Deal_inv(k);
         }
 }
 int C(int n,int m)
 {
         return (s64)Jc[n]*inv[m]%MOD*inv[n-m]%MOD;
 }

 int ways(int i,int j)
 {
         return C(a[j].x+a[j].y-a[i].x-a[i].y, a[j].x-a[i].x);
 }

 void Moit(int &a)
 {
         if(a<) a+=MOD;
         if(a>MOD) a-=MOD;
 }

 int main()
 {
         n=get();    m=get();    K=get();    S=get();

         A[]=S;    for(a_num=;a_num<=;a_num++) S=(S+)/, A[a_num]=S;
         D::pre(n+m);

            for(int i=;i<=K;i++)
         {
             a[i].x=get();    a[i].y=get();
         }
         a[++K].x = n;    a[K].y = m;
         sort(a+,a+K+,cmp);

         for(int i=;i<=K;i++)
         {
             for(int j=;j<a_num;j++)
             {
                 f[i][j] = C(a[i].x+a[i].y-,a[i].x-);
                 for(int k=;k<=i-;k++)
                 {
                     if(a[k].x <= a[i].x && a[k].y <= a[i].y)
                     f[i][j] -= (s64)f[k][j] * ways(k,i) % MOD,
                     Moit(f[i][j]);
                 }

                 for(int k=;k<=j-;k++)
                     f[i][j] -= f[i][k], Moit(f[i][j]);
             }
         }

         int All = C(n+m-,n-);

         for(int i=;i<a_num;i++)
         {
             Up = (Up + (s64)f[K][i]*A[i]) % MOD;
             All -= f[K][i]; Moit(All);
         }

         Up = Up + All;    Moit(Up);

         printf("%d",(s64)Up * D::Quickpow(C(n+m-,n-),MOD-) % MOD);
 }