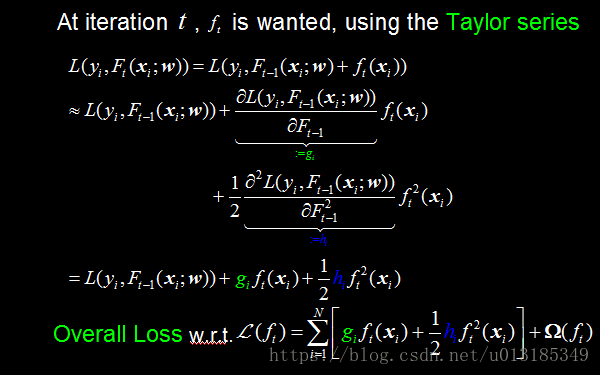GBDT && XGBOOST
GBDT && XGBOOST
Outline
Introduction
GBDT Model
XGBOOST Model
GBDT vs. XGBOOST
Experiments
References
Introduction
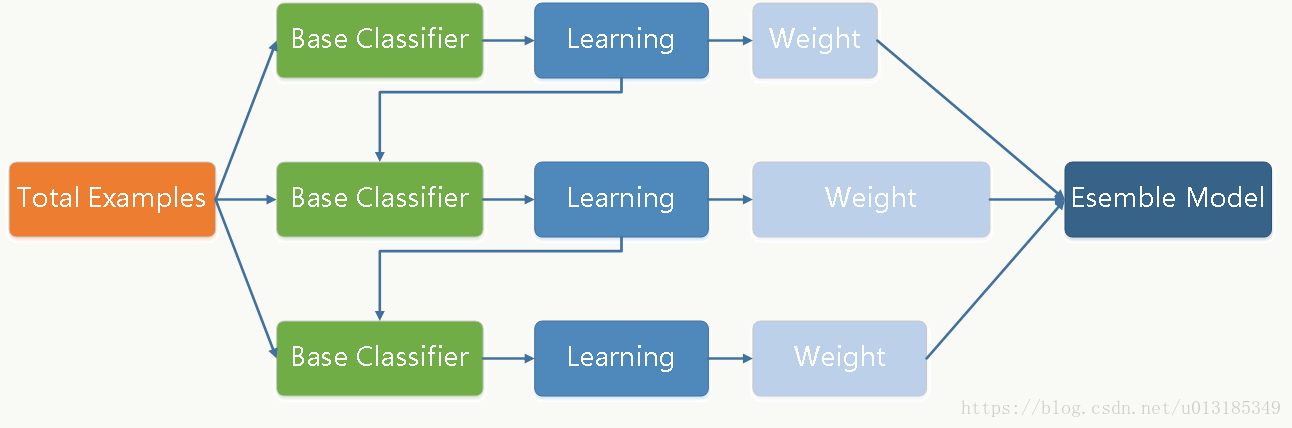
Gradient Boosting Decision Tree is a machine learning technique for regression and classification problems, which produces a prediction model in the form of an ensemble of basic learning models, typically decision trees.
Decision Tree: e.g.
eXtreme Gradient Boosting (XGBOOST) is an efficient implementation of Gradient Boosting method, a scalable, portable and distributed GB library, and it was started as a research project by Tianqi Chen.
GBDT Model
XGBOOST Model
GBDT vs XGBOOST:
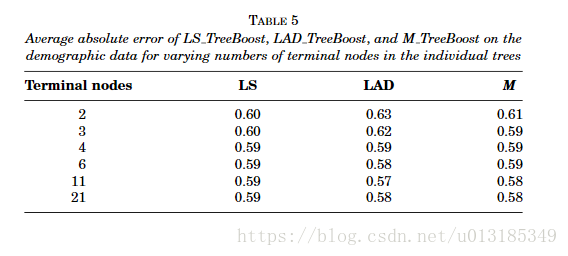
Experiments
References:
1. J. Friedman(1999). Greedy Function Approximation: A Gradient Boosting
Machine.
2. J. Friedman(1999). Stochastic Gradient Boosting.
3. T. Chen, C. Guestrin(2016). XGBoost: A Scalable Tree Boosting System.
GBDT && XGBOOST的更多相关文章
- RF/GBDT/XGBoost/LightGBM简单总结(完结)
这四种都是非常流行的集成学习(Ensemble Learning)方式,在本文简单总结一下它们的原理和使用方法. Random Forest(随机森林): 随机森林属于Bagging,也就是有放回抽样 ...
- RF,GBDT,XGBoost,lightGBM的对比
转载地址:https://blog.csdn.net/u014248127/article/details/79015803 RF,GBDT,XGBoost,lightGBM都属于集成学习(Ensem ...
- 机器学习 GBDT+xgboost 决策树提升
目录 xgboost CART(Classify and Regression Tree) GBDT(Gradient Boosting Desicion Tree) GB思想(Gradient Bo ...
- gbdt xgboost 贼难理解!
https://www.zybuluo.com/yxd/note/611571 https://zhuanlan.zhihu.com/p/29765582 gbdt 在看统计学习方法的时候 理解很吃力 ...
- GBDT XGBOOST的区别与联系
Xgboost是GB算法的高效实现,xgboost中的基学习器除了可以是CART(gbtree)也可以是线性分类器(gblinear). 传统GBDT以CART作为基分类器,xgboost还支持线性分 ...
- 机器学习相关知识整理系列之三:Boosting算法原理,GBDT&XGBoost
1. Boosting算法基本思路 提升方法思路:对于一个复杂的问题,将多个专家的判断进行适当的综合所得出的判断,要比任何一个专家单独判断好.每一步产生一个弱预测模型(如决策树),并加权累加到总模型中 ...
- 机器学习之——集成算法,随机森林,Bootsing,Adaboost,Staking,GBDT,XGboost
集成学习 集成算法 随机森林(前身是bagging或者随机抽样)(并行算法) 提升算法(Boosting算法) GBDT(迭代决策树) (串行算法) Adaboost (串行算法) Stacking ...
- 机器学习总结(一) Adaboost,GBDT和XGboost算法
一: 提升方法概述 提升方法是一种常用的统计学习方法,其实就是将多个弱学习器提升(boost)为一个强学习器的算法.其工作机制是通过一个弱学习算法,从初始训练集中训练出一个弱学习器,再根据弱学习器的表 ...
- 常见算法(logistic回归,随机森林,GBDT和xgboost)
常见算法(logistic回归,随机森林,GBDT和xgboost) 9.25r早上面网易数据挖掘工程师岗位,第一次面数据挖掘的岗位,只想着能够去多准备一些,体验面这个岗位的感觉,虽然最好心有不甘告终 ...
随机推荐
- JavaEE权限管理系统的搭建(五)--------RBAC权限管理中的权限菜单的显示
上一小节实现了登录的实现,本小节实现登录后根据用户名查询当前用户的角色所关联的所有权限,然后进行菜单的显示.登录成功后,如下图所示,管理设置是一级菜单,管理员列表,角色管理,权限管理是二级菜单. 先来 ...
- 学习WebSocket笔记
由于HTTP协议是无状态的,服务器只会响应来自客户端的请求,但是它与客户端之间不具备持续连接. 当用户在浏览器上进行操作时,可以请求服务器上的api:但是反过来不可以:服务端发生了一件事,无法将这个事 ...
- Shiro 登录认证源码详解
Shiro 登录认证源码详解 Apache Shiro 是一个强大且灵活的 Java 开源安全框架,拥有登录认证.授权管理.企业级会话管理和加密等功能,相比 Spring Security 来说要更加 ...
- iOS之ShareSDK各社交平台申请AppKey的网址及申请流程汇总
平台 开放平台地址 APPkey 申请流程 新浪微博 http://open.weibo.com http://bbs.mob.com/thread-89-1-4.html 新浪微博开放平台接入tip ...
- js中FormData+XMLHttpRequest数据传输
前言: 首先我们需要了解,前后端进行数据传输依赖于浏览器的XMLHttpRequest对象 一.什么是XMLHttpRequest对象? XMLHttpRequest 是DOM对象,提供了对于http ...
- CF练习记录
2018/5/6 Codeforces Round #478 (Div. 2) C http://codeforces.com/contest/975/problem/C Valhalla Siege ...
- python一个小程序:猜数字
猜数字游戏程序运行示例: I am thinking of a number between 1 and 20. Take a guess. 8 Your guess is too low. Take ...
- npm install 报错
今天准备在服务器上部署一下pm2,发现 npm install -g pm2 爆出了错误 error Unexpected end of JSON input while parsing near ...
- Java : java基础(4) 线程
java开启多线程的方式,第一种是新建一个Thread的子类,然后重写它的run()方法就可以,调用类的对象的start()方法,jvm就会新开一个线程执行run()方法. 第二种是类实现Runabl ...
- 方别《QQ群霸屏技术》,又见《QQ群建群细则》
规则,时刻变动;QQ群系列,咱们再来一轮. QQ群霸屏技术,你说建群貌似很菜,大家仿佛都知道,其实只知其一不知其二. QQ群类别 群分类,常规的就以下几种. 普通群. 建群随意,偏个性化,一言不合就拉 ...