hdu 3648 Median Filter (树状数组)

Median Filter

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1092    Accepted Submission(s): 269

Problem Description

Median filter is a cornerstone of modern image processing and is used extensively in

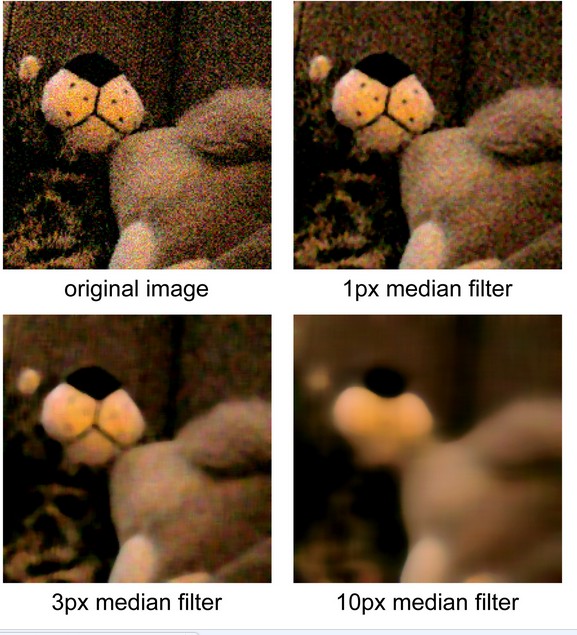
Given a black and white image of n by n pixels, the algorithm works as follow:
For each pixel p at the i‐th row and the j‐th column (1+ r <= i, j <= n – r), its gray level g[i,j] is replace by the median of gray levels of pixels in the (2r+1) by (2r+1) square centered at p. The square is called the filtering window and r is its radius.

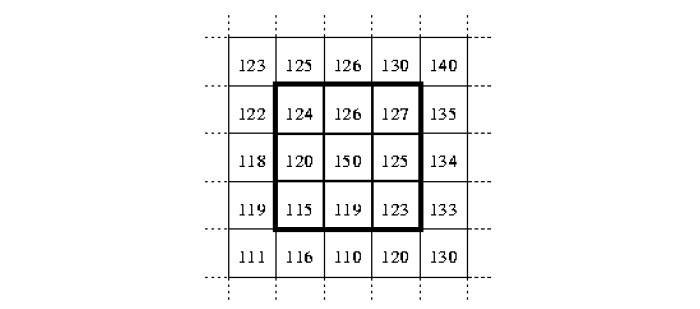
Considering the above example, the gray level of the pixel at center will be changed from 150 to 124, which is the median of a filtering window of radius 1.

Note that the algorithm won’t be applied on the pixels near the boundary, for the filtering window lies outside the image. So you are actually asked to output the filtered sub-image which contains the pixels from (r+1, r+1) to (n-r, n-r).

 

Input

The input contains several test cases.
For each test case:

(a) The first line contains two integers, n and r, meaning that the size of image is n * n (3 <= n <= 500) and the radius of filtering window is r ( 3 <= 2r + 1 <= n).

(b) The following n lines contains the n by n gray level matrix presenting the image

(c) The gray level ranges from 0 to 1000000 The input ends by double 0s.

 

Output

For each test case output a (n – 2r) by (n – 2r) matrix presenting the sub-image after filtered.

 

Sample Input

3 1

1 1 1

1 1 1

1 1 1

3 1

1 9 6

4 5 2

3 7 8

3 1

0 0 0

255 255 255

0 255 0

5 1

0 0 1 1 0

1 0 1 0 1

0 0 1 1 1

1 1 1 0 1

1 0 0 0 1

0 0

 

Sample Output

1

5

0

0 1 1

1 1 1

1 0 1

Hint

The definition of “median”: One type of average, found by arranging the values in order and then selecting the one in the middle.
If the total number of values in the sample is even, then the median is the mean of the two middle numbers.
The median is a useful number in cases where the distribution has very large extreme values which would otherwise skew the data.

 

Source

2010 Asia Regional Hangzhou Site —— Online Contest

 

Recommend

lcy   |   We have carefully selected several similar problems for you:  3641 3649 3647 3646 3645 

 

题意：

中值滤波，求在n*n的矩阵中，内(n-2*r)*(n-2*r)的中值滤波后的子矩阵。

中值滤波的方式就是对于每一个可以取到的以(i,j)为矩阵中心的(2*r+1)*(2*r+1)的子矩阵，将子矩阵中所有数排序后的中位数作为新值，新值不影响后面的值。

做法：

树状数组

这是一题比较有趣的题吧，一开始暴力试一下是TLE的，明显算法复杂都会很大。子矩阵的处理如果用到排序应该都会超时，因此看到了一个很高效的算法，就是利用树状数组和一个在树状树组中求第k大的数的函数，后来在采用S行遍历，代码因此有点长，还要注意一下输出。

 //1781MS    6196K    2399 B    G++
 #include<stdio.h>
 #include<string.h>
 #define N 505
 int g[N][N];
 int ans[N][N];
 int c[<<];
 int n,r,M;
 inline int lowbit(int k)
 {
     return k&(-k);
 }
 int getsum(int k)
 {
     int s=;
     for(;k>;k-=lowbit(k))
         s+=c[k];
     return s;
 }
 void insert(int k,int detal)
 {
     for(;k<=M;k+=lowbit(k))
         c[k]+=detal;
 }
 int find_kth(int k) //树状数组找第k大的数
 {
     int sum=,pos=;
     for(int i=;i>=;i--){
         pos+=(<<i);
         if(pos>M || sum+c[pos]>=k)
             pos-=(<<i);
         else sum+=c[pos];
     }
     return pos+;
 }
 void solve()
 {
     int R=*r+;
     int k=R*R/+;
     for(int i=;i<=R;i++)
         for(int j=;j<=R;j++)
             insert(g[i][j],);
     //for(int i=1;i<=2*(k-1);i++) printf("*%d\n",c[i]);
     for(int i=r+;i<=n-r;i++){
         if((i-r)&){  //奇数行，向右遍历
             if(i!=r+){
                 for(int j=;j<=R;j++){
                     insert(g[i-r-][j],-);
                     insert(g[i+r][j],);
                 }
             }
             ans[i][r+]=find_kth(k);
             for(int j=r+;j<=n-r;j++){
                 for(int ii=i-r;ii<=i+r;ii++){
                     insert(g[ii][j-r-],-);
                     insert(g[ii][j+r],);
                 }
                 ans[i][j]=find_kth(k);
             }
         }else{ //偶数行，向左遍历
             for(int j=n;j>=n-R+;j--){
                 insert(g[i-r-][j],-);
                 insert(g[i+r][j],);
             }
             ans[i][n-r]=find_kth(k);
             for(int j=n-r-;j>=r+;j--){
                 for(int ii=i-r;ii<=i+r;ii++){
                     insert(g[ii][j+r+],-);
                     insert(g[ii][j-r],);
                 }
                 ans[i][j]=find_kth(k);
             }
         }
     }
 }
 int main(void)
 {
     while(scanf("%d%d",&n,&r),n+r)
     {
         M=;
         memset(c,,sizeof(c));
         for(int i=;i<=n;i++)
             for(int j=;j<=n;j++){
                 scanf("%d",&g[i][j]);
                 g[i][j]++;
                 if(g[i][j]>M) M=g[i][j];
             }
         solve();
         for(int i=r+;i<=n-r;i++)
             for(int j=r+;j<=n-r;j++)
                 printf(j==n-r?"%d \n":"%d ",ans[i][j]-);
     }
     return ;
 }

 /*

 3 1
 1 9 6
 4 5 2
 3 7 8

 5 1
 0 0 1 1 0
 1 0 1 0 1
 0 0 1 1 1
 1 1 1 0 1
 1 0 0 0 1

 */