旅行商问题（Traveling Salesman Problem,TSP)的+Leapms线性规划模型及c++调用

知识点

旅行商问题的线性规划模型
旅行商问题的+Leapms模型及CPLEX求解
C++调用+Leapms

旅行商问题

旅行商问题是一个重要的NP-难问题。一个旅行商人目前在城市1，他必须对其余n-1个城市访问且仅访问一次而后回到城市1，请规

划其最短的循环路线。

旅行商问题的建模

设城市i,j之间的距离为D[i][j]，又设0-1变量x[i][j]表示从城市i到城市j的道路是否在循环路线上。于是旅行商问题的目标可以被写成：

min sum{i=1,...,n;j=1,...,n;i<>j}(D[i][j] x[i][j])

因每个城市必须被访问一次且仅被访问一次，于是对每个城市需要进入一次且仅一次，而且出去一次且仅一次，于是有以下两个约束：

sum{i=1,...,n;i<>j} x[i][j] = 1 | j=2,...,n
sum{j=1,...,n;i<>j} x[i][j] = 1 | i=2,...,n

仅采用以上约束时，结果会形成多个不联通的循环。为防止这种情况，为每个城市规定一个访问循序的编号u[i]变量。u[i]=k表示该城市是第k个被访问的城市。规定u[0]=1，任意u[i]<=n-1。显然如果x[i][j]=1，即道路 i,j 被选定在循环路径中，则u[j]>=u[i]+1。用以下约束表达这个逻辑：

u[j]>=u[i]+1-n(1-x[i][j])|i=1,...,n;j=2,...,n;i<>j

上式中，如果x[i][j]=1, 则等价于u[j]>=u[i]+1。如果x[i][j]=0，则右端小于等于0，恒小于等于左端，相当于该约束不存在。

旅行商问题的Leapms模型

使用Cd表示城市的地理坐标，则问题的Leapms模型为

//The Traveling Salesman Problem
min sum{i=1,...,n;j=1,...,n;i<>j} x[i][j] D[i][j]
subject to
	sum{i=1,...,n;i<>j} x[i][j] = 1 | j=2,...,n
	sum{j=1,...,n;i<>j} x[i][j] = 1 | i=2,...,n

	u[1]=0
	u[j]>=u[i]+1-n(1-x[i][j])|i=1,...,n;j=2,...,n;i<>j
	u[i]<=n-1|i=1,...,n
where
	n is an integer
	Cd is a set
	D[i][j] is a number|i=1,...,n;j=1,...,n
	x[i][j] is a variable of binary|i=1,...,n;j=1,...,n;i<>j
	u[i] is a variable of nonnegative number|i=1,...,n
data_relation
	n=_$(Cd)/2
	D[i][j]=sqrt((Cd[2i-1]-Cd[2j-1])^2+(Cd[2i]-Cd[2j])^2) -->
		|i=1,...,n;j=1,...,n
data
	Cd={
		0 0
		1062 182
		1028 503
		206 200
		473 291
		1741 233
	}//六个城市

使用mip或者cplex命令瞬间可以求解上述模型

Welcome to +Leapms ver 1.1(162260) Teaching Version  -- an LP/LMIP modeling and
solving tool.欢迎使用利珀 版本1.1(162260) Teaching Version  -- LP/LMIP 建模和求
解工具.

+Leapms>load
 Current directory is "ROOT".
 .........
        current.leap
        tsp.leap
        tsp_tamplet.leap
 .........
please input the filename:tsp
================================================================
1:  //The Traveling Salesman Problem
2:  min sum{i=1,...,n;j=1,...,n;i<>j} x[i][j] D[i][j]
3:  subject to
4:      sum{i=1,...,n;i<>j} x[i][j] = 1 | j=2,...,n
5:      sum{j=1,...,n;i<>j} x[i][j] = 1 | i=2,...,n
6:
7:      u[1]=0
8:      u[j]>=u[i]+1-n(1-x[i][j])|i=1,...,n;j=2,...,n;i<>j
9:      u[i]<=n-1|i=1,...,n
10:  where
11:     n is an integer
12:     Cd is a set
13:     D[i][j] is a number|i=1,...,n;j=1,...,n
14:     x[i][j] is a variable of binary|i=1,...,n;j=1,...,n;i<>j
15:     u[i] is a variable of nonnegative number|i=1,...,n
16:  data_relation
17:     n=_$(Cd)/2
18:     D[i][j]=sqrt((Cd[2i-1]-Cd[2j-1])^2+(Cd[2i]-Cd[2j])^2) -->
19:             |i=1,...,n;j=1,...,n
20:  data
21:     Cd={
22:             0 0
23:             1062 182
24:             1028 503
25:             206 200
26:             473 291
27:             1741 233
28:             1815 633
29:             1060 916
30:     }//八个城市
31:
================================================================
>>end of the file.
Parsing model:
1D
2R
3V
4O
5C
6S
7End.
..................................
number of variables=64
number of constraints=72
..................................
+Leapms>mip
relexed_solution=3006.07; number_of_nodes_branched=0; memindex=(2,2)
 nbnode=138;  memindex=(26,26) zstar=4880.76; GB->zi=4802.4
 nbnode=337;  memindex=(24,24) zstar=4328.8; GB->zi=4802.4
 nbnode=513;  memindex=(12,12) zstar=4112.39; GB->zi=4549.03
 nbnode=697;  memindex=(16,16) zstar=4541.65; GB->zi=4549.03
The Problem is solved to optimal as an MIP.
找到整数规划的最优解.非零变量值和最优目标值如下：
  .........
    u2* =1
    u3* =5
    u4* =7
    u5* =6
    u6* =2
    u7* =3
    u8* =4
    x1_2* =1
    x2_6* =1
    x3_5* =1
    x4_1* =1
    x5_4* =1
    x6_7* =1
    x7_8* =1
    x8_3* =1
  .........
    Objective*=4549.03
  .........
+Leapms>

 C++调用+Leapms模型

直接的+leapms求解得到的是变量的结果数据，如果要进一步处理，则使用高级语言调用则更加方便。

+Leapms提供了c_leap类可以做此工作。主要的函数是:

c_leap::loadleap(char *leapfile) -- 调入名为leapfile的leapms模型

c_leap::mip() -- 求解当前的leapms模型(使用leapms自带求解器,功能较弱)

c_leap::cplex() -- 求解当前的leapms模型（使用CPLEX求解器）

c_leap::getObj() -- 返回当前最优解的目标值

c_leap::getVar(char *varname) -- 返回变量名为varname的值

c_leap::getVar(char *varname，int nid, int id1,...) -- 返回变量名为varname，脚标个数为nid, 脚标分别为id1,...的变量的值。

把城市坐标数据放在loc.txt中，下面的c++代码可以根据leapms模型模板（即去掉data段的旅行商问题leapms模型）生成当前模型、求解当前模型，并输出autocad批处理图形脚本。

#include<iostream>
#include<fstream>
#include "leap.h"
using namespace std;

int m;
double x[3000],y[3000];

//实例化leap对象
c_leap lp;			

//读原始数据生成当前模型
bool genModel(string fmodel,string fdata){
	ifstream iff;
	ofstream off;

	//复制模板到当前模型current.leap中
	iff.open(fmodel);
	off.open("current.leap");
	if(!iff||!off)return false;
	string line;
	while(getline(iff,line)){
		off<<line<<endl;
	}
	iff.close();

	//读入数据文件添加到当前模型的数据区
	iff.open(fdata);
	if(!iff)return false;

	off<<"data"<<endl<<"\tCd={"<<endl;
	int i=0;
	while(!iff.eof()){
		iff>>x[i]>>y[i];
		off<<"\t\t"<<x[i]<<" "<<y[i]<<endl;
		i++;
	}
	m=i;
	off<<"\t}"<<endl;

	iff.close();
	off.close();

	//结束模型生成过程
	return true;
}

//输出图形
void draw(){

	ofstream ocad;
	ocad.open("tsp.scr");
	if(!ocad){
		cout<<"\t输出图形错误！"<<endl;
		return;
	}

	for(int i=0;i<m;i++){
		ocad<<"color 7"<<endl;
		ocad<<"point "<<x[i]<<","<<y[i]<<endl;
		for(int j=0;j<m;j++){
			if(i==j)continue;
			if(lp.getVar("x",2,i+1,j+1)>0){
				ocad<<"color 1"<<endl;
				ocad<<"line "<<x[i]<<","<<y[i]<<" "<<x[j]<<","<<y[j]<<" "<<endl;
			}
		}

	}
	ocad.close();
}

int main(){

	//读原始数据生成当前模型
	if(!genModel("tsp_tamplet.leap","loc.txt")){
		cout<<"\t错误！不能打开文件！"<<endl;
		return -1;
	}

	//调入模型
	lp.loadLeap("current.leap");	

	//使用cplex求解模型的整数解
	lp.cplex();	

	//输出旅行商路径图形
	draw();

	//结束程序
	return 0;
}

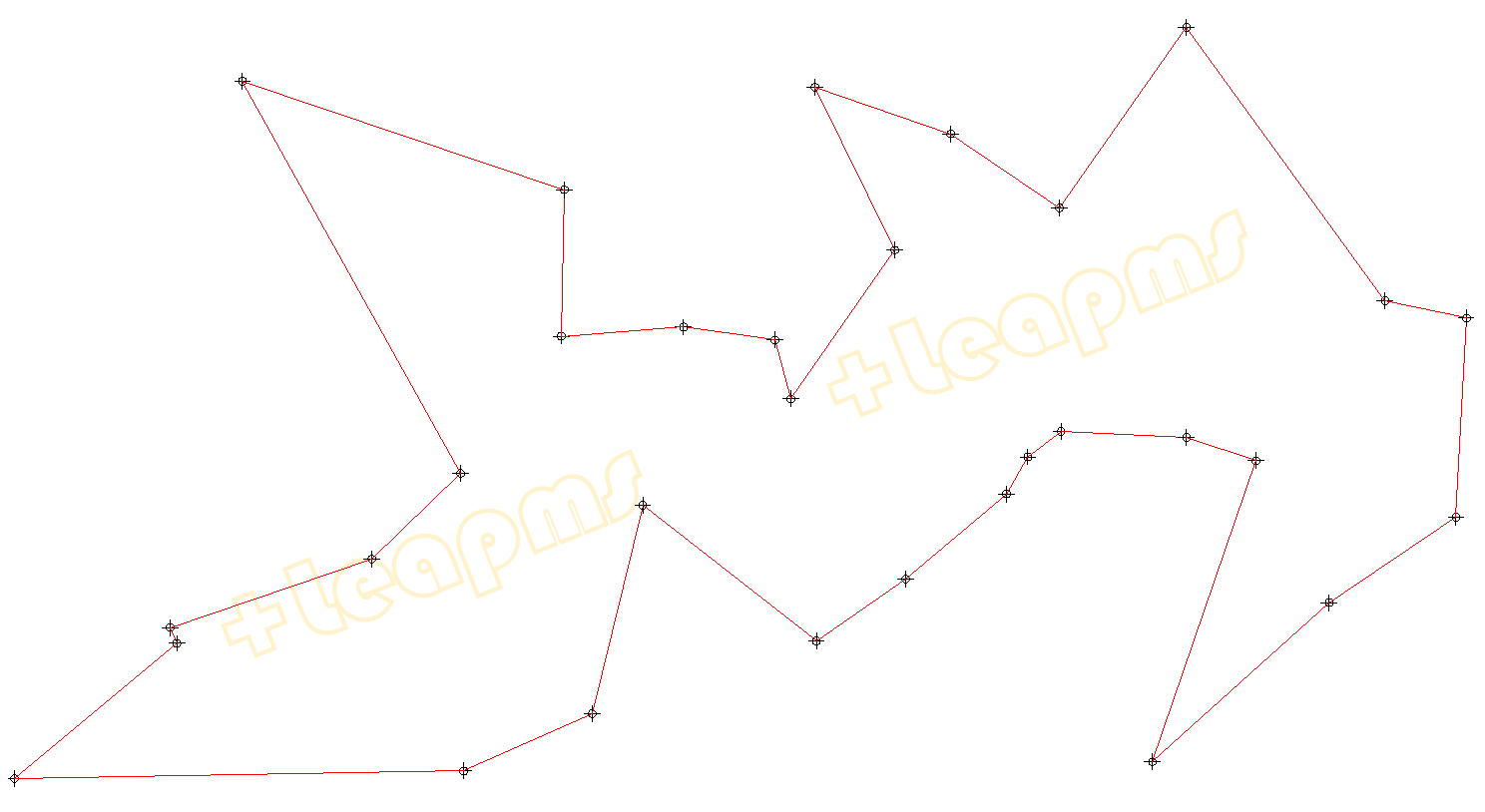
对31个城市TSP问题的求解结果

城市分布

巡回路线