OneHotEncoder独热编码和 LabelEncoder标签编码

学习sklearn和kagggle时遇到的问题，什么是独热编码？为什么要用独热编码？什么情况下可以用独热编码？以及和其他几种编码方式的区别。

首先了解机器学习中的特征类别：连续型特征和离散型特征

拿到获取的原始特征，必须对每一特征分别进行归一化，比如，特征A的取值范围是[-1000,1000]，特征B的取值范围是[-1,1].如果使用logistic回归，w1*x1+w2*x2，因为x1的取值太大了，所以x2基本起不了作用。所以，必须进行特征的归一化，每个特征都单独进行归一化。

对于连续性特征：

• Rescale bounded continuous features: All continuous input that are bounded, rescale them to [-1, 1] through x = (2x - max - min)/(max - min).    线性放缩到[-1,1]
• Standardize all continuous features: All continuous input should be standardized and by this I mean, for every continuous feature, compute its mean (u) and standard deviation (s) and do x = (x - u)/s.       放缩到均值为0，方差为1

对于离散性特征：

• Binarize categorical/discrete features: 对于离散的特征基本就是按照one-hot（独热）编码，该离散特征有多少取值，就用多少维来表示该特征。

一. 什么是独热编码？

独热码，在英文文献中称做 one-hot code, 直观来说就是有多少个状态就有多少比特，而且只有一个比特为1，其他全为0的一种码制。举例如下：

假如有三种颜色特征：红、黄、蓝。 在利用机器学习的算法时一般需要进行向量化或者数字化。那么你可能想令 红=1，黄=2，蓝=3. 那么这样其实实现了标签编码，即给不同类别以标签。然而这意味着机器可能会学习到“红<黄<蓝”，但这并不是我们的让机器学习的本意，只是想让机器区分它们，并无大小比较之意。所以这时标签编码是不够的，需要进一步转换。因为有三种颜色状态，所以就有3个比特。即红色：1 0 0 ，黄色: 0 1 0，蓝色：0 0 1 。如此一来每两个向量之间的距离都是根号2，在向量空间距离都相等，所以这样不会出现偏序性，基本不会影响基于向量空间度量算法的效果。

自然状态码为：000,001,010,011,100,101

独热编码为：000001,000010,000100,001000,010000,100000

来一个sklearn的例子：

from sklearn import preprocessing
enc = preprocessing.OneHotEncoder()
enc.fit([[0, 0, 3], [1, 1, 0], [0, 2, 1], [1, 0, 2]])    # fit来学习编码
enc.transform([[0, 1, 3]]).toarray()    # 进行编码

输出：array([[ 1.,  0.,  0.,  1.,  0.,  0.,  0.,  0.,  1.]])

数据矩阵是4*3，即4个数据，3个特征维度。

0 0 3                      观察左边的数据矩阵，第一列为第一个特征维度，有两种取值0\1. 所以对应编码方式为10 、01

1 1 0                                               同理，第二列为第二个特征维度，有三种取值0\1\2，所以对应编码方式为100、010、001

0 2 1                                               同理，第三列为第三个特征维度，有四中取值0\1\2\3，所以对应编码方式为1000、0100、0010、0001

1 0 2

再来看要进行编码的参数[0 , 1,  3]， 0作为第一个特征编码为10,  1作为第二个特征编码为010， 3作为第三个特征编码为0001.  故此编码结果为 1 0 0 1 0 0 0 0 1

二. 为什么要独热编码？

正如上文所言，独热编码（哑变量 dummy variable）是因为大部分算法是基于向量空间中的度量来进行计算的，为了使非偏序关系的变量取值不具有偏序性，并且到圆点是等距的。使用one-hot编码，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点。将离散型特征使用one-hot编码，会让特征之间的距离计算更加合理。离散特征进行one-hot编码后，编码后的特征，其实每一维度的特征都可以看做是连续的特征。就可以跟对连续型特征的归一化方法一样，对每一维特征进行归一化。比如归一化到[-1,1]或归一化到均值为0,方差为1。

为什么特征向量要映射到欧式空间？

将离散特征通过one-hot编码映射到欧式空间，是因为，在回归，分类，聚类等机器学习算法中，特征之间距离的计算或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算，计算余弦相似性，基于的就是欧式空间。

三 .独热编码优缺点

• 优点：独热编码解决了分类器不好处理属性数据的问题，在一定程度上也起到了扩充特征的作用。它的值只有0和1，不同的类型存储在垂直的空间。
• 缺点：当类别的数量很多时，特征空间会变得非常大。在这种情况下，一般可以用PCA来减少维度。而且one hot encoding+PCA这种组合在实际中也非常有用。

四. 什么情况下(不)用独热编码？

• 用：独热编码用来解决类别型数据的离散值问题，
• 不用：将离散型特征进行one-hot编码的作用，是为了让距离计算更合理，但如果特征是离散的，并且不用one-hot编码就可以很合理的计算出距离，那么就没必要进行one-hot编码。 有些基于树的算法在处理变量时，并不是基于向量空间度量，数值只是个类别符号，即没有偏序关系，所以不用进行独热编码。  Tree Model不太需要one-hot编码： 对于决策树来说，one-hot的本质是增加树的深度。

总的来说，要是one hot encoding的类别数目不太多，建议优先考虑。

五.  什么情况下(不)需要归一化？

• 需要： 基于参数的模型或基于距离的模型，都是要进行特征的归一化。
• 不需要：基于树的方法是不需要进行特征的归一化，例如随机森林，bagging 和 boosting等。

六.  标签编码LabelEncoder

作用： 利用LabelEncoder() 将转换成连续的数值型变量。即是对不连续的数字或者文本进行编号例如：

from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
le.fit([1,5,67,100])
le.transform([1,1,100,67,5])

输出： array([0,0,3,2,1])

>>> le = preprocessing.LabelEncoder()
>>> le.fit(["paris", "paris", "tokyo", "amsterdam"])
LabelEncoder()
>>> list(le.classes_)
['amsterdam', 'paris', 'tokyo']     # 三个类别分别为0 1 2
>>> le.transform(["tokyo", "tokyo", "paris"])
array([2, 2, 1]...)
>>> list(le.inverse_transform([2, 2, 1]))   # 逆过程
['tokyo', 'tokyo', 'paris']

限制：上文颜色的例子已经提到标签编码了。Label encoding在某些情况下很有用，但是场景限制很多。再举一例：比如有[dog,cat,dog,mouse,cat]，我们把其转换为[1,2,1,3,2]。这里就产生了一个奇怪的现象：dog和mouse的平均值是cat。所以目前还没有发现标签编码的广泛使用。

附：基本的机器学习过程

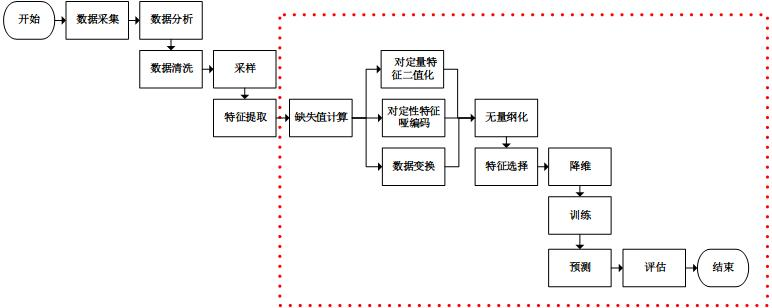
参考：

Quora：What are good ways to handle discrete and continuous inputs together?

数据预处理：独热编码（One-Hot Encoding）

使用sklearn优雅地进行数据挖掘

数据挖掘比赛通用框架

Label Encoding vs One Hot Encoding

[scikit-learn] 特征二值化编码函数的一些坑