哈夫曼（Huffman)树和哈夫曼编码

一、哈夫曼（Huffman)树和哈夫曼编码

1.哈夫曼树（Huffman)又称最优二叉树，是一类带权路径长度最短的树， 常用于信息检测。

定义：

结点间的路径长度:树中一个结点到另一个结点之间分支数目称为这对结点之间的路径长度。

树的路径长度:树的根结点到树中每一结点的路径长度之和。

带权路径长度:从根结点到某结点的路径长度与该结点上权的乘积。

树的带权路径长度:树中所有叶子结点的带权路径长度之和记为WPL。

例如：

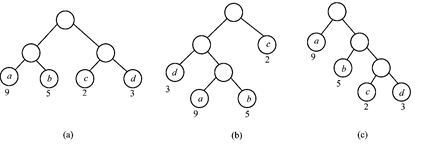
对图（a）: WPL =9×2+5×2+2×2+3×2=38

对图（b）: WPL =3×2+9×3+5×3+2×1=50

对图（c）: WPL =9×1+5×2+2×3+3×3=34

总结:

路径长度最短的二叉树，其带权路径长度不一定最短;

带权路径最短的二叉树，其结点权值越大离根越近;

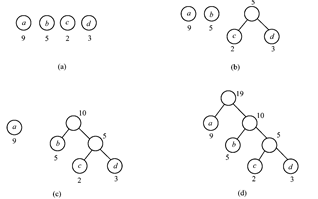
2. 哈夫曼树的构造

（1） 根据给定的 n个权值｛W1 ，W2 ，…，Wn ｝构成n棵二叉树的集合F=｛T1 ，T 2 ，…，Tn ｝，其中每棵二叉树中只有一个带权为Wi 的根结点。

（2） 在 F中选择两棵根结点最小的树作为左、右子树构造一棵新的二叉树T， 且置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。

（3） 将新二叉树T加入二叉树集合 F中，从二叉树集合F中 去除原来两棵根结点权    值最小的树。

（4） 重复（2）和（3）步直到 F 中只含有一棵树为止，这棵树就是哈夫曼树。

3. 哈夫曼编码

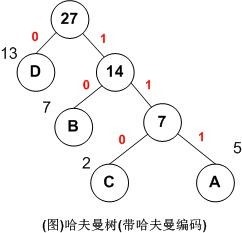
树中从根到每个叶子节点都有一条路径，对路径上的各分支约定指向左子树的分支表示”0”码，指向右子树的分支表示“1”码，取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码，即是哈夫曼编码。

利用哈夫曼树，不仅能构造出前缀编码，而且还能使电文编码的总长度最短。

拿图例子来说：

A，B，C，D对应的哈夫曼编码分别为：111，10，110，0