TensorFlow tensor张量拼接concat - split & stack - unstack

TensorFlow提供两种类型的拼接：

tf.concat(values, axis, name='concat')：按照指定的已经存在的轴进行拼接
tf.stack(values, axis=0, name='stack')：按照指定的新建的轴进行拼接

concat

t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0) ==> [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
== t1.expand(t2)
tf.concat([t1, t2], 1) ==> [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]]

stack

t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.stack([t1, t2], 0)  ==> [[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]]
x = []; x.append(t1); x.append(t2)

tf.stack([t1, t2], 1)  ==> [[[1, 2, 3], [7, 8, 9]], [[4, 5, 6], [10, 11, 12]]]
tf.stack([t1, t2], 2)  ==> [[[1, 7], [2, 8], [3, 9]], [[4, 10], [5, 11], [6, 12]]]

x = tf.constant([1, 4])
y = tf.constant([2, 5])
z = tf.constant([3, 6])
tf.stack([x, y, z])  　　　　 # [[1, 4], [2, 5], [3, 6]] (Pack along first dim.)
tf.stack([x, y, z], axis=1)  # [[1, 2, 3], [4, 5, 6]]

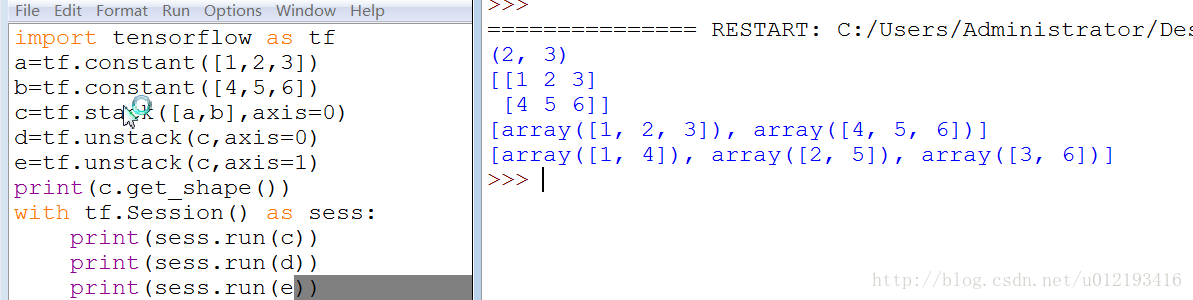
UnStack