luogu P3722 [AH2017/HNOI2017]影魔

传送门

我太弱了,只会乱搞,正解是不可能正解的,这辈子不可能写正解的，太蠢了又想不出什么东西，就是乱搞这种东西，才能维持得了做题这样子

考虑将询问离线,按右端点排序,并且预处理出每个位置往前面第一个大于这个数的位置,记为\(fa_i\)

如果加入一个右端点\(i\),那么可以加上贡献的左端点有以下三类

• 在区间\([fa_i,i)\)中,从\(i-1\)开始一直跳\(fa\),能到达的位置加上p1

• 在区间\([fa_i,i)\)中,从\(i-1\)开始一直跳\(fa\),不能到达的位置加上p2

• 在区间\([1,fa_i)\)中,从\(fa_i\)开始一直跳\(fa\),能到达的位置加上p2

看下图把qwq(黑色代表没加上贡献,绿色代表加上p1,红色代表加上p2)

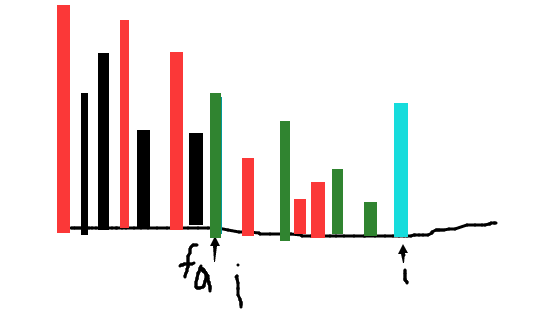
每次移动右端点,对应的询问答案就是询问区间内的权值和

代码极差,慎看

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define LL long long
#define il inline
#define re register
#define db double

using namespace std;
const int N=200000+10,M=240000+10;
il int rd()
{
  int x=0,w=1;char ch=0;
  while(ch<'0'||ch>'9') {if(ch=='-') w=-1;ch=getchar();}
  while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
  return x*w;
}
struct sgmtr
{
#define lc (o<<1)
#define rc ((o<<1)|1)
#define mid ((l+r)>>1)
  LL a[M<<2];
  int lz[M<<2];
  il void psup(int o){a[o]=a[lc]+a[rc];}
  il void ad(int o,int l,int r,int x){a[o]+=1ll*x*(r-l+1),lz[o]+=x;}
  il void psdn(int o,int l,int r)
  {
    if(lz[o]) ad(lc,l,mid,lz[o]),ad(rc,mid+1,r,lz[o]),lz[o]=0;
  }
  void modif(int o,int l,int r,int ll,int rr,int x)
  {
    if(ll<=l&&r<=rr)
      {
        ad(o,l,r,x);
        return;
      }
    psdn(o,l,r);
    if(ll<=mid) modif(lc,l,mid,ll,rr,x);
    if(rr>mid) modif(rc,mid+1,r,ll,rr,x);
    psup(o);
  }
  int quer(int o,int l,int r,int ll,int rr)
  {
    if(ll<=l&&r<=rr) return a[o];
    int an=0;
    psdn(o,l,r);
    if(ll<=mid) an+=quer(lc,l,mid,ll,rr);
    if(rr>mid) an+=quer(rc,mid+1,r,ll,rr);
    psup(o);
    return an;
  }
}tr[2];
int to[N],nt[N],hd[N],tot;
il void add(int x,int y){++tot,to[tot]=y,nt[tot]=hd[x],hd[x]=tot;}
int n,m,p1,p2,a[N],fa[N],top[N];
LL an[N];
void dfs(int x,int ntp)
{
  top[x]=ntp;
  for(int i=hd[x];i;i=nt[i]) dfs(to[i],to[i]==x+1?ntp:to[i]);
}
struct qu
{
  int l,r,id;
  bool operator < (const qu &bb) const {return r<bb.r;}
}qq[N];
int st[N],tp;

int main()
{
  n=rd(),m=rd(),p1=rd(),p2=rd();
  for(int i=1;i<=n;++i)
    {
      a[i]=rd();
      while(tp&&a[st[tp]]<a[i]) --tp;
      fa[i]=st[tp];
      st[++tp]=i;
    }
  for(int i=n;i;--i) add(fa[i],i);
  dfs(0,0);
  for(int i=1;i<=m;++i) qq[i].l=rd(),qq[i].r=rd(),qq[i].id=i;
  sort(qq+1,qq+m+1);
  for(int i=1,r=0;i<=m;++i)
    {
      while(r<qq[i].r)
        {
          ++r;
          tr[1].modif(1,0,n,fa[r],r-1,1);
          int x=r-1;
          while(x)
            {
              tr[0].modif(1,0,n,top[x],x,1);
              tr[1].modif(1,0,n,top[x],x,-1);
              x=fa[top[x]];
            }
          x=fa[fa[r]];
          while(x)
            {
              tr[0].modif(1,0,n,top[x],x,-1);
              tr[1].modif(1,0,n,top[x],x,2);
              x=fa[top[x]];
            }
        }
      int l=qq[i].l;
      an[qq[i].id]=1ll*p1*(tr[0].quer(1,0,n,0,r-1)-tr[0].quer(1,0,n,0,l-1))+1ll*p2*(tr[1].quer(1,0,n,0,r-1)-tr[1].quer(1,0,n,0,l-1));
    }
  for(int i=1;i<=m;++i) printf("%lld\n",an[i]);
  return 0;
}

或者来Orzyyb