P、NP、NPC、NP-Hard问题到底是何方神圣？

最近在做一个求解有向图中回路的问题，老师说求解图中全部回路是一个NP难问题。突然想到P、NP、NPC、NP-hard的描述一致不是很清楚，所以又学习了一下。

在解释这四个概念之前，我们需要先知道两个问题多项式时间和规约，我们首先来看多项式时间，一个算法可以在多项式时间内解决即指一个算法的时间复杂度是为多项式——\(ax^n+bx^{n-1}+\cdots+x+c\)，例如\(o(1)、o(ln n)、o(n^a)\)等，我们成为多项式级复杂度，而\(o(a^n)\)这类指数级复杂度我们称之为非多项式级复杂度。

再看规约，问题A可以约化为问题B，称为“问题A可规约为问题B”，可以理解为问题B的解一定就是问题A的解，因此解决A不会难于解决B。由此可知问题B的时间复杂度一定大于等于问题A。《算法导论》中有一个例子，现在有两个问题：求解一个一元一次方程和求解一个一元二次方程。那么我们说，前者可以规约为后者，意即知道如何解一个一元二次方程那么一定能解出一元一次方程。我们可以写出两个程序分别对应两个问题，那么我们能找到一个“规则”，按照这个规则把解一元一次方程程序的输入数据变一下，用在解一元二次方程的程序上，两个程序总能得到一样的结果。这个规则即是：两个方程的对应项系数不变，一元二次方程的二次项系数为0。

P类问题(Polynomial)

P类问题，由其名字（Polynomial）我们不难看出它指的就是能在多项式时间内解决的问题，亦即解决这个问题的算法的时间复杂度是是多项式。

NP问题(Non-deterministic Polynomial)

在多项式时间内可判定其答案是否正确的问题。也就是说，不能判定这个问题是否能在多项式时间内求得其解，但是对于这个问题的一个解可以在多项式时间内证明是否正确的。即该问题的求解过程是不确定的，而对其某一个解的验证则能够在多项式时间内完成。因而显然P类问题是NP问题的子集，因为倘若一个问题可以在多项式时间内被求解，那么这个解也一定可以在多项式时间内被验证是否正确。

NP-Complete问题

存在这样一个NP问题，所有的NP问题都可以规约成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。所以显然这个问题需要满足两个条件:
-它是一个NP问题
-所有的NP问题都可以规约成它

NP-Hard问题

NP难问题：NP-Hard问题是这样一种问题，它满足NPC问题定义的第二条但不一定要满足第一条（就是说，NP-Hard问题要比 NPC问题的范围广，NP-Hard问题没有限定属于NP），即所有的NP问题都能约化到它，但是他不一定是一个NP问题。NP-Hard问题同样难以找到多项式的算法，但它不列入我们的研究范围，因为它不一定是NP问题。即使NPC问题发现了多项式级的算法，NP-Hard问题有可能仍然无法得到多项式级的算法。事实上，由于NP-Hard放宽了限定条件，它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。

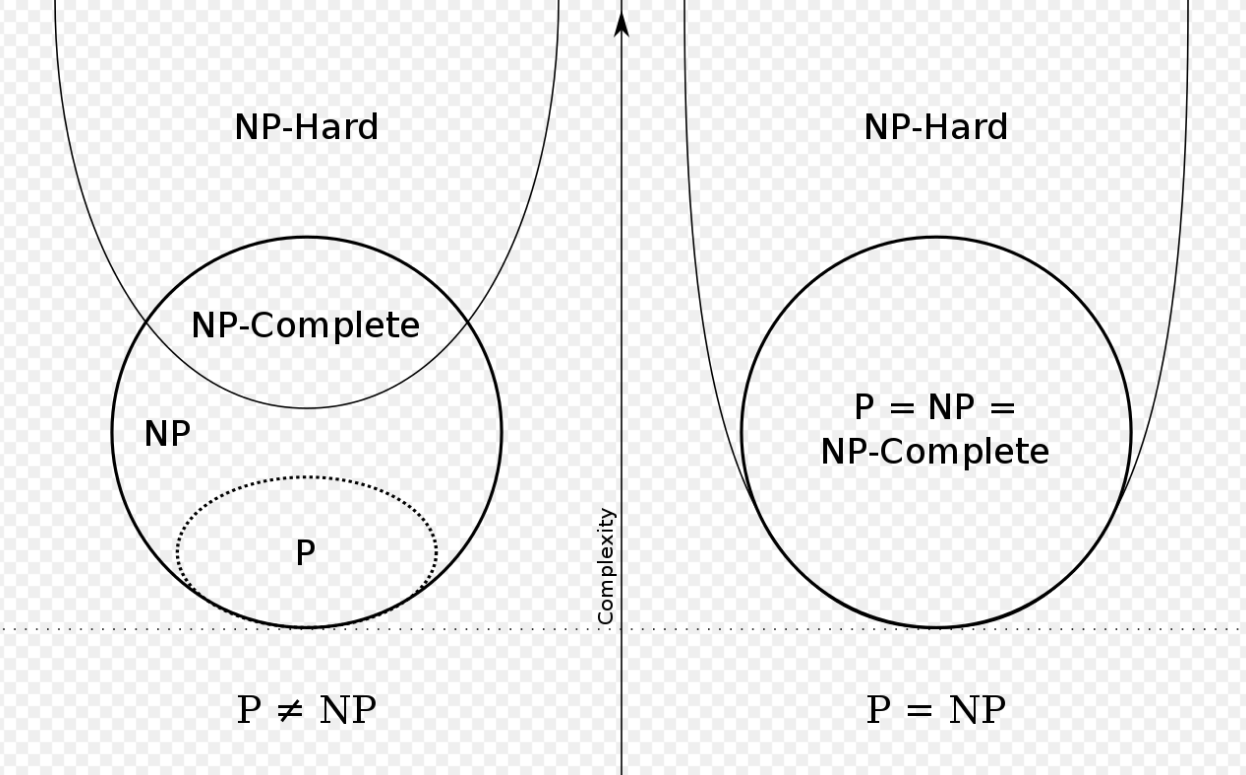
所以这四类问题的关系用图像表示即：

参考资料
算法导论
https://en.wikipedia.org/wiki/NP-hardness