[matlab] 19.matlab 基础几何学

polyshape 

函数可创建由二维顶点定义的多边形，并返回具有描述其顶点、实心区域和孔的各种属性的 polyshape 对象。例如，pgon = polyshape([0 0 1 1],[1 0 0 1]) 将创建由四个点 (0,1)、(0,0)、(1,0) 和 (1,1) 定义的实心正方形。

pgon = polyshape(x,y) 从由 x 坐标向量和对应的 y 坐标向量定义的二维顶点创建 polyshape。x 和 y 的长度必须相同，且至少要有三个元素。

pgon = polyshape([0 0 1 1],[1 0 0 1]);
figure(4)
plot(pgon)

polyshape 二维多边形构建

nsidedpoly 正多边形

pgon = nsidedpoly(n,Name,Value)

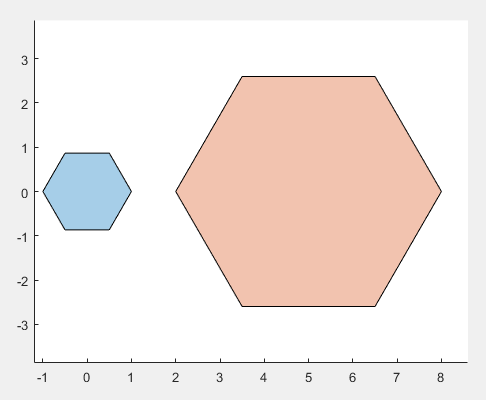
pgon1 = nsidedpoly(6);
pgon2 = nsidedpoly(6,'Center',[5 0],'SideLength',3);
figure(4)
plot([pgon1 pgon2])
axis equal

nsidedpoly(正多边形)

polyarea 计算多边形的面积

L = linspace(0,2.*pi,100);
xv = 1.2*cos(L)';
yv = 1.2*sin(L)';
xx=1.1*cos(L)';
yy=1.1*sin(L)';
AA=polyshape(xv,yv);
AAA=polyshape(xx,yy);

plot(AA);
hold on;
plot(AAA);
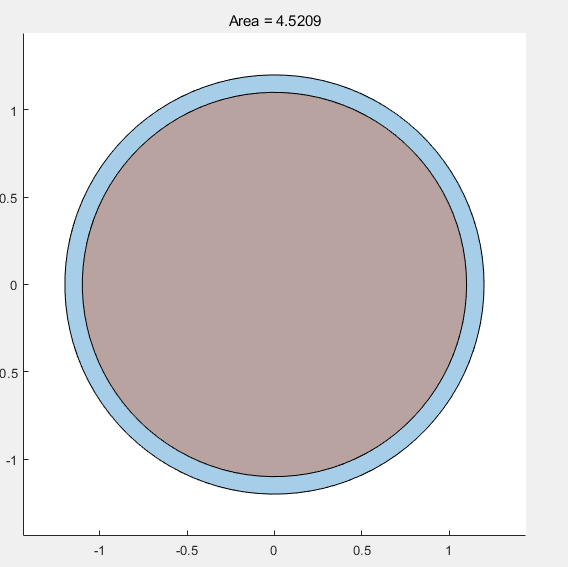
title(['Area = ' num2str(A)])
axis image

A = polyarea(xv,yv)  %计算面积

polyarea 计算多边形面积

inpolygon 位于多边形区域边缘内部或边缘上的点

in = inpolygon(xq,yq,xv,yv)  返回 in，以指明 xq 和 yq 所指定的查询点是在 xv 和 yv 定义的多边形区域的边缘内部还是在边缘上

[in,on] = inpolygon(xq,yq,xv,yv) 还返回 on 以指明查询点是否位于多边形区域的边缘。

clc,clear all;
L = linspace(0,2.*pi,100);
xv1 = 1.2*cos(L)';
yv1 = 1.2*sin(L)';
xv2=0.4*cos(L)';
yv2=0.4*sin(L)';

Round1=polyshape(xv1,yv1);
Round2=polyshape(xv2,yv2);
Round1Area = polyarea(xv1,yv1)
Round2Area = polyarea(xv2,yv2)

rng default  %恢复matlab启动时默认的全局随机流
xq = randn(250,1);  %随机生成250个正态分布点
yq = randn(250,1);  %随机生成250个正态分布点

in = inpolygon(xq,yq,xv1,yv1);  % numel(xq(in))查看在几何体内部的数量
figure(4)
plot(Round1); %画第一个圆
hold on;
plot(Round2); %画第二个圆
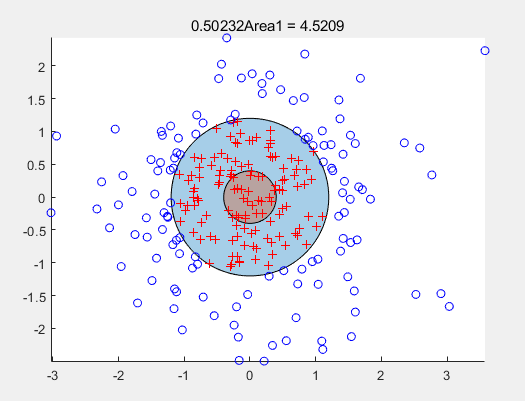
plot(xq(in),yq(in),'r+') % 标记在内部的点
plot(xq(~in),yq(~in),'bo') % 标记在外部的点
hold off
title(['Area1,Area2 = ' num2str(Round1Area),num2str(Round2Area)])
axis equal
axis image

凸多边形内的点

axes('xlim',[0 10],'ylim',[0 10])
a=[1 1 2 2];
b=[3 4 5 6];
c=[1 1 3 3];
figure
rectangle('position',a,'EdgeColor', 'r');
rectangle('position',b,'EdgeColor', 'b');
rectangle('position',c,'EdgeColor', 'k');

area_ab = rectint(a,b)
area_ac = rectint(a,c)

rectint 矩形交叉区域

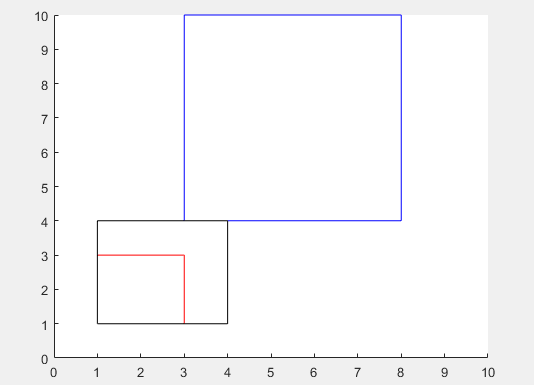
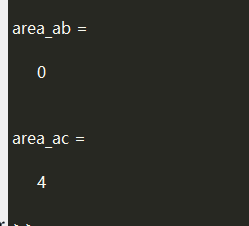
area = rectint(A,B) 返回位置向量 A 和 B 指定的矩形的交叉区域。

如果 A 和 B 分别指定一个矩形，则输出 area 为标量。

A 和 B 还可以是矩阵，其中每行是一个位置向量。area 是一个矩阵，为 B 指定的所有矩形提供 A 指定的所有矩阵的交叉区域。即，如果 A 是 n×4 并且 B 是 m×4，则 area 是 n×m 矩阵，其中 area(i,j) 是 A 的第 i 行和 B 的第 j 行指定的矩形的交叉区域。

a=1;b=1.5;d=0:360;
x=a*cosd(d);
y=b*sind(d);
figure(1),cla
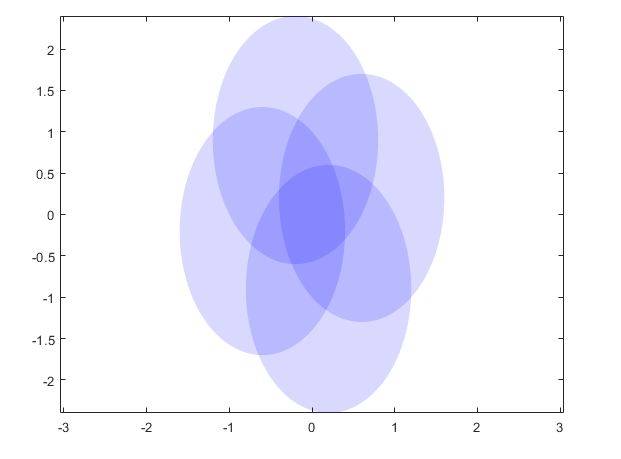
patch(x+0.6,y+0.2,'b','edgecolor','none','facealpha',0.15);%不透明度0.15
patch(x-0.6,y-0.2,'b','edgecolor','none','facealpha',0.15);%不透明度0.15
patch(x-0.2,y+0.9,'b','edgecolor','none','facealpha',0.15);%不透明度0.15
patch(x+0.2,y-0.9,'b','edgecolor','none','facealpha',0.15);%不透明度0.15
axis equal
box on;
set(gcf,'color','w');

半透明重叠加深 patch函数

v1 = [2 4; 2 8; 8 4];
f1 = [1 2 3];
figure
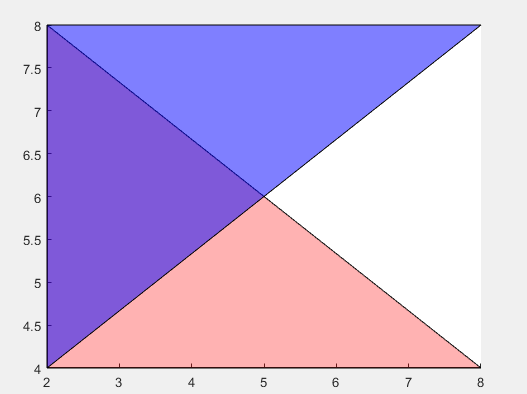
patch('Faces',f1,'Vertices',v1,'FaceColor','red','FaceAlpha',.3);

v2 = [2 4; 2 8; 8 8];
f2 = [1 2 3];
patch('Faces',f2,'Vertices',v2,'FaceColor','blue','FaceAlpha',.5);

通过将 FaceAlpha 属性设置为 0 和 1 之间的值，创建两个半透明的多边形。

boundary 二维或三维空间内的一组点的边界

x = gallery('uniformdata',3000,1,1);
y = gallery('uniformdata',3000,1,10);

plot(x,y,'k.')
xlim([-0.3 1.2])
ylim([-0.3 1.2])
k = boundary(x,y); %返回一个表示包围点 (x,y) 的单个相容二维边界的点索引向量。收缩因子为1
hold on;
line(x(k),y(k),'color','b'); 

j = boundary(x,y,0.01); %收缩因子为0.1  最大为1 越大包裹性越紧
line(x(j),y(j),'color','r');

[~, vol] = boundary(x,y);  %包围点形成的形状的体积 或 面积
axis equal;
vol %返回 包围的体积或者面积

boundary 二维或三维空间内的一组点的边界

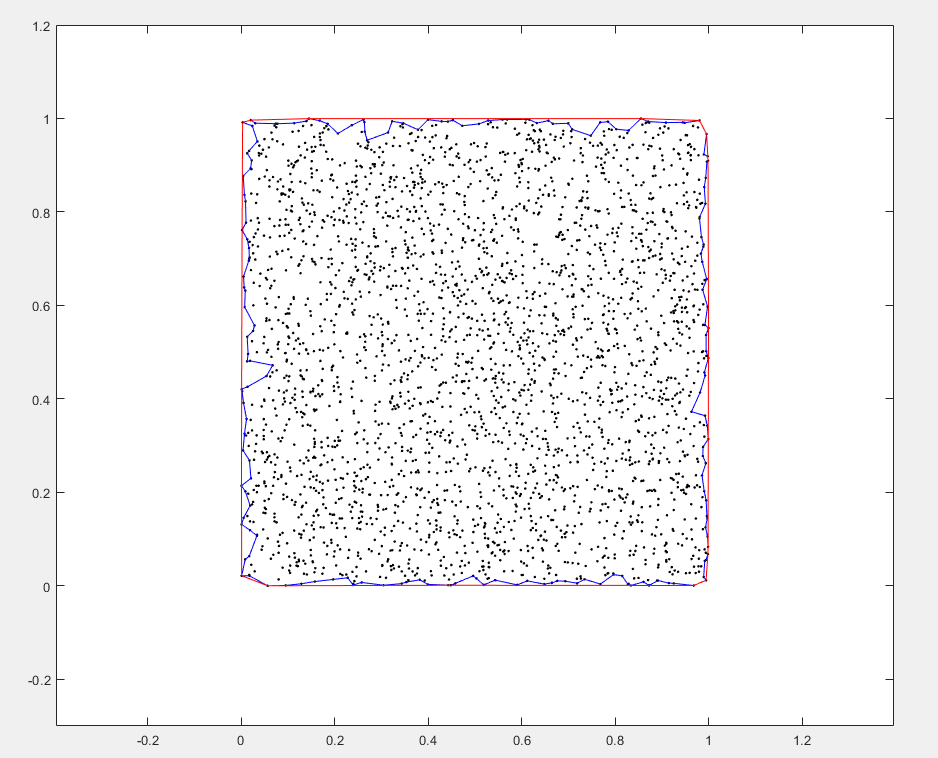
[~, vol] = boundary(x,y); %包围点形成的形状的体积
axis equal;
vol 可以输出二维平面 各个点包围的面积

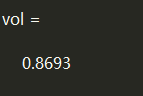
P = gallery('uniformdata',30,3,5);
subplot(1,2,1);
plot3(P(:,1),P(:,2),P(:,3),'.','MarkerSize',10)
axis equal;
grid on
k = boundary(P);
hold on
subplot(1,2,2);
trisurf(k,P(:,1),P(:,2),P(:,3),'Facecolor','red','FaceAlpha',0.1)  %收缩因子默认0
[~, vol] = boundary(P);  %包围点形成的形状的体积
axis equal;
vol %体积

三维

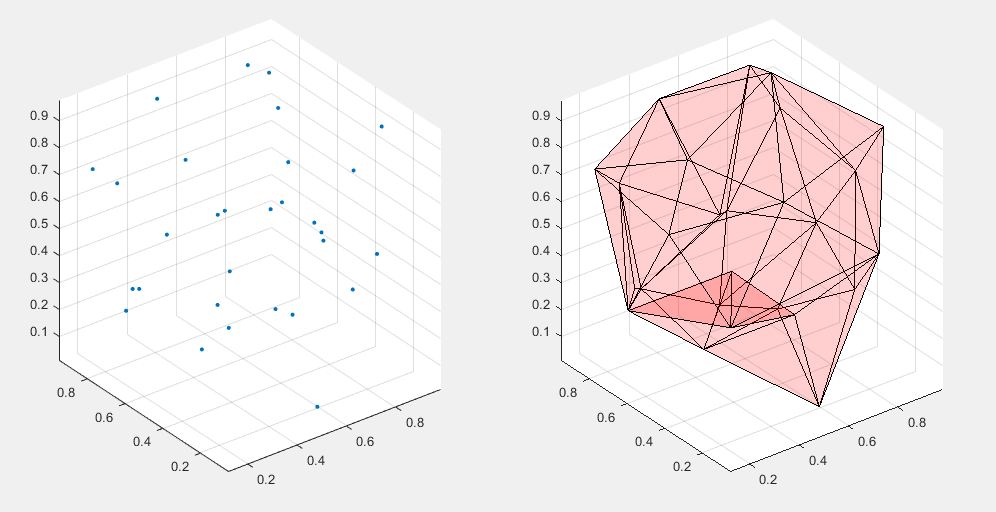
[~, vol] = boundary(P);   vol 返回体积

convhull 凸包

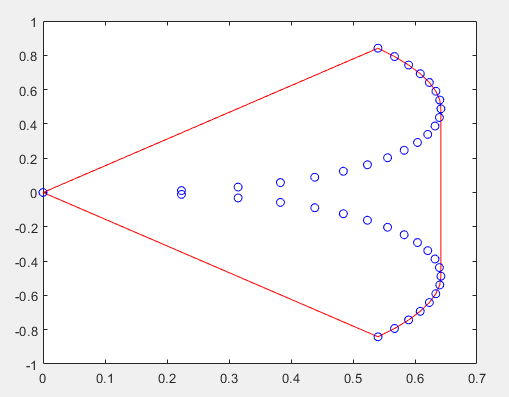
xx = -1:.05:1;
yy = abs(sqrt(xx));
[x,y] = pol2cart(xx,yy);
k = convhull(x,y);
plot(x(k),y(k),'r-',x,y,'bo')

二维凸包

alphaShape 依据二维和三维中的点构建的多边形和多面体

th = (pi/12:pi/12:2*pi)';
x1 = [reshape(cos(th)*(1:5), numel(cos(th)*(1:5)),1); 0];
y1 = [reshape(sin(th)*(1:5), numel(sin(th)*(1:5)),1); 0];
x = [x1; x1+15];
y = [y1; y1];
subplot(1,2,1)
plot(x,y,'.')
axis equal
subplot(1,2,2)
shp = alphaShape(x,y); %默认 alpha 半径可生成带不规则边界的 alpha 形状。
shp.Alpha = 2.5; % 要更好地捕获点集边界，请尝试更大的alpha 半径。
plot(shp)
axis equal

alphaShape alphaShape 创建一个可将一组二维或三维点包围起来的边界面或三维体。

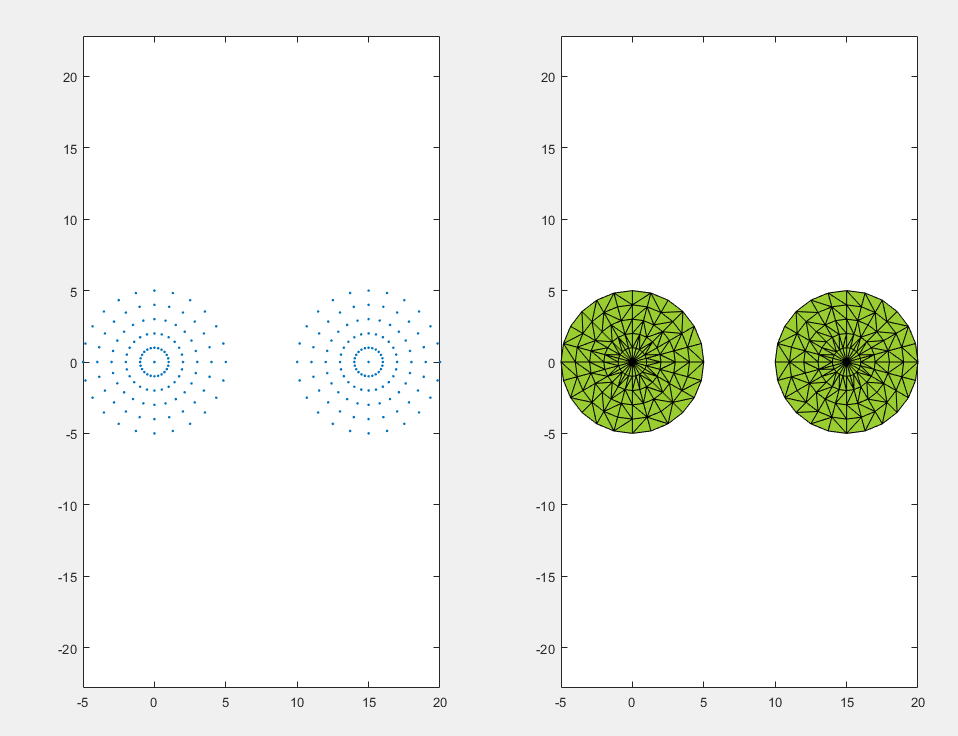
delaunayTriangulation

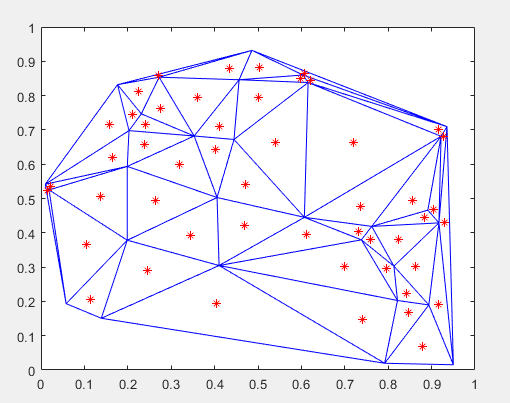
使用 delaunayTriangulation 对象可以基于一组点创建二维或三维 Delaunay 三角剖分。对于二维数据，您也可以指定边约束。

P = gallery('uniformdata',[30 2],0);
DT = delaunayTriangulation(P);
IC = incenter(DT);
triplot(DT) %绘制 Delaunay 三角剖分
hold on
plot(IC(:,1),IC(:,2),'*r') 

绘图