hdu 3944 DP? 组合数取模(Lucas定理+预处理+帕斯卡公式优化)

DP?

Problem Description

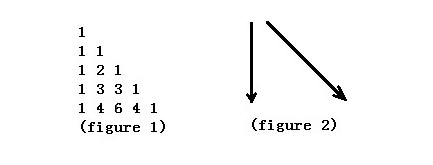
Figure
1 shows the Yang Hui Triangle. We number the row from top to bottom
0,1,2,…and the column from left to right 0,1,2,….If using C(n,k)
represents the number of row n, column k. The Yang Hui Triangle has a
regular pattern as follows.
C(n,0)=C(n,n)=1 (n ≥ 0)
C(n,k)=C(n-1,k-1)+C(n-1,k) (0<k<n)
Write
a program that calculates the minimum sum of numbers passed on a route
that starts at the top and ends at row n, column k. Each step can go
either straight down or diagonally down to the right like figure 2.
As the answer may be very large, you only need to output the answer mod p which is a prime.

 

Input

Input
to the problem will consists of series of up to 100000 data sets. For
each data there is a line contains three integers n,
k(0<=k<=n<10^9) p(p<10^4 and p is a prime) . Input is
terminated by end-of-file.

 

Output

For
every test case, you should output "Case #C: " first, where C indicates
the case number and starts at 1.Then output the minimum sum mod p.

 

Sample Input

1 1 2

4 2 7

 

Sample Output

Case #1: 0

Case #2: 5

 

思路:Lucas定理正好适用于p较小的组合数取模问题；由于很多组查询，所以只能预处理出每个素数对应的每个每个值的阶乘值；

Lucas定理:C(n,m)=C([n/p],[m/p]) * C(a0,b0)  (mod p);

这是我们能容易地求解出终点的值，但是如果我们是一层一层地加到边界，再找还有多少个1?这样直接T了，现在就需要帕斯卡公式还计算这个sigma和了；

帕斯卡公式:

1.  C(n+1,m) = C(n,m) + C(n-1,m-1)+...+C(n-m,0);  当m <= n/2时，斜向上走到左边界，之后还有n - m个1

2.  C(n+1,m+1) = C(n-1,m) + C(n-2,m)+...+C(n-m,m); 一直竖直向上走到右边界，之后还有m个1

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<vector>
#include<cmath>
#include<stdlib.h>
#include<time.h>
#include<stack>
#include<set>
#include<map>
#include<queue>
using namespace std;
#define rep0(i,l,r) for(int i = (l);i < (r);i++)
#define rep1(i,l,r) for(int i = (l);i <= (r);i++)
#define rep_0(i,r,l) for(int i = (r);i > (l);i--)
#define rep_1(i,r,l) for(int i = (r);i >= (l);i--)
#define MS0(a) memset(a,0,sizeof(a))
#define MS1(a) memset(a,-1,sizeof(a))
#define MSi(a) memset(a,0x3f,sizeof(a))
#define inf 0x3f3f3f3f
#define lson l, m, rt << 1
#define rson m+1, r, rt << 1|1
typedef pair<int,int> PII;
#define A first
#define B second
#define MK make_pair
typedef __int64 ll;
template<typename T>
void read1(T &m)
{
    T x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    m = x*f;
}
template<typename T>
void read2(T &a,T &b){read1(a);read1(b);}
template<typename T>
void read3(T &a,T &b,T &c){read1(a);read1(b);read1(c);}
template<typename T>
void out(T a)
{
    if(a>) out(a/);
    putchar(a%+'');
}
const int N = ;
int prime[N],check[N];
void getprime()
{
    for(int i = ;i < N;i++)if(!check[i]){
        prime[i] = ++prime[];
        for(int j = i*i;j < N;j += i)
            check[j] = ;
    }
}
int f[][N];
void init()
{
    getprime();
    for(int i = ;i <= N;i++){
        if(prime[i] == ) continue;
        int id = prime[i];
        f[id][] = ;
        for(int j = ;j < N;j++)
            f[id][j] = f[id][j-]*j%i;
    }
}
int pow_mod(int a,int n,int p)
{
    int ans = ;
    while(n){
        if(n & ) ans = ans*a%p;
        a = a*a%p;
        n >>= ;
    }
    return ans;
}
int C(int n,int m,int p)
{
    if(n < m) return ;
    if(n == m) return ;
    int id = prime[p];
    int a = f[id][n],b = f[id][m]*f[id][n - m]%p;
    return a*pow_mod(b,p-,p)%p;
}
int Lucas(int n,int m,int p)
{
    if(m == ) return ;
    if(m == ) return n%p;
    return C(n%p,m%p,p)*Lucas(n/p,m/p,p)%p;
}
int main()
{
    init();
    int n,m,p,kase = ;
    while(scanf("%d%d%d",&n,&m,&p) == ){
        if(m <= n/) m = n - m;
        int ans = Lucas(n + ,m + ,p);
        printf("Case #%d: %d\n",kase++,(ans + m)%p);
    }
    return ;
}