POJ 2549 Sumsets

Sumsets

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 10593		Accepted: 2890

Description

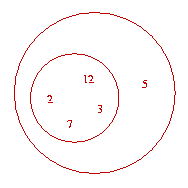Given S, a set of integers, find the largest d such that a + b + c = d where a, b, c, and d are distinct elements of S.

Input

Several S, each consisting of a line containing an integer 1 <= n <= 1000 indicating the number of elements in S, followed by the elements of S, one per line. Each element of S is a distinct integer between -536870912 and +536870911 inclusive. The last line of input contains 0.

Output

For each S, a single line containing d, or a single line containing "no solution".

Sample Input

5
2
3
5
7
12
5
2
16
64
256
1024
0

Sample Output

12
no solution

Source

Waterloo local 2001.06.02

 

 

 

解析：折半枚举。之前碰到的折半枚举都是将集合折半，这次不同，折半的思想体现在等式上。将等式a + b + c = d转化为a + b = d - c，等式分成左右两部分，预处理出左右两部分，将左半部分排序，然后枚举右半部分，二分查找即可。时间复杂度为O(n²logn²)。

 

 

 

#include <cstdio>
#include <algorithm>
using namespace std;

const int MAXN = 1000+5;
int n;
int a[MAXN];

struct S{
    int val;
    int i, j;
    bool operator < (const S& b)const
    {
        return val < b.val;
    }
};
S l[MAXN*MAXN], r[MAXN*MAXN];

bool ok(S& a, S& b)
{
    return a.i != b.i && a.j != b.j && a.i != b.j && a.j != b.i;
}

void solve()
{
    int lcnt = 0;
    for(int i = 0; i < n; ++i){
        for(int j = i+1; j < n; ++j){
            l[lcnt].val = a[i]+a[j];
            l[lcnt].i = i;
            l[lcnt++].j = j;
        }
    }
    int rcnt = 0;
    for(int i = 0; i < n; ++i){
        for(int j = i+1; j < n; ++j){
            r[rcnt].val = a[i]-a[j];
            r[rcnt].i = i;
            r[rcnt++].j = j;
            r[rcnt].val = a[j]-a[i];
            r[rcnt].i = j;
            r[rcnt++].j = i;
        }
    }
    sort(l, l+lcnt);
    int res = 0xffffffff;
    for(int i = 0; i < rcnt; ++i){
        int d = lower_bound(l, l+lcnt, r[i])-l;
        if(ok(l[d], r[i]) && l[d].val == r[i].val){
            res = max(res, r[i].val+a[r[i].j]);
        }
    }
    if(res == 0xffffffff)
        printf("no solution\n");
    else
        printf("%d\n", res);
}

int main()
{
    while(scanf("%d", &n), n){
        for(int i = 0; i < n; ++i)
            scanf("%d", &a[i]);
        solve();
    }
    return 0;
}