小橙书阅读指南（十三）——连通性算法（union-find）

上一章我大概说明了什么是图论以及无向图的基础概念，本章我们要研究一种更普遍的算法——连通性算法。它属于图论的分支，也是一种抽象算法。在深入算法之前，我们先提出一个具体的问题：假设在空间中存在N个点，我们可以通过线段连接任意两点，相互连接的点属于同一组连通分量，我们如何计算点p和点q之间是否连通。算法的核心是：如何表示连通性以及如何检查连通性。

下面提供算法的抽象接口：

/**
 * 连通性算法
 */
public interface UnionFind {
    /**
     * p点和q点之间添加一条通路
     *
     * @param p
     * @param q
     */
    void union(int p, int q);
 
    /**
     * 获取p点的连通分量
     *
     * @param p
     * @return
     */
    int find(int p);
 
    /**
     * 判断p点和q点是否存在一条通路
     *
     * @param p
     * @param q
     * @return
     */
    boolean connected(int p, int q);
 
    /**
     * 连通分量的数量
     *
     * @return
     */
    int count();
}

一、快速查询算法Quick-Find

我们将空间中的点这一概念抽象成int[]（整形数组)，i代表不同的点int[i]代表不同的连通分量。一种比较容易理解的想法是，从属于同一组连通分量的任一点p和q必定int[p]等于int[q]。因此当我们需要查询点p和q是否连通的时候只需要判断int[p] == int[q]是否成立即可。

/**
 * 连通性算法：quick-find
 */
public class QuickFind implements UnionFind {
    private int[] id; // 分量id
    private int count;
 
    public QuickFind(int n) {
        count = n;
        id = new int[n];
        for (int i = 0; i < n; i++) {
            id[i] = i;
        }
    }
 
    @Override
    public void union(int p, int q) {
        int pID = find(p);
        int qID = find(q);
 
        if(pID == qID) {
            return;
        }
        for(int i = 0;i < id.length; i++) {
            if(id[i] == pID) {
                id[i] = qID;
            }
        }
        count--;
    }
 
    @Override
    public int find(int p) {
        return id[p];
    }
 
    @Override
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
 
    @Override
    public int count() {
        return count;
    }
}

find()操作的速度显然是很快的，因为它只需要访问id[]数组一次。但是对于每一对数组union()都需要扫描整个id[]数组。因此quick-find算法一般无法处理大型数组。

算法图示：

二、快速连接算法Quick-Union

我们要讨论的下一个算法的重点是提高union()方法的速度，为此可能会稍微牺牲一下find()的效率，但是通常情况下这样做是值得的。Quick-Union算法考虑把属于同一组连通分量的点连接成一棵树，i代表点，int[i]代表i的父节点，根节点p等于int[p]。

public class QuickUnion implements UnionFind {
    private int count;
    private int[] id;
 
    public QuickUnion(int n) {
        count = n;
        id = new int[n];
        for(int i = 0; i < n; i++) {
            id[i] = i;
        }
    }
    @Override
    public void union(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if(pRoot == qRoot) {
            return;
        }
 
        id[pRoot] = qRoot;
        count--;
    }
 
    @Override
    public int find(int p) {
        while(p != id[p]) {
            p = id[p];
        }
        return p;
    }
 
    @Override
    public boolean connected(int p, int q) {
        return false;
    }
 
    @Override
    public int count() {
        return 0;
    }
}

快速连接算法的每一次连接会分别遍历两次连通分量，在连通分量中包含元素数量相对总数而言比较小的情况下可以提供非常不错的速度。

算法图示：

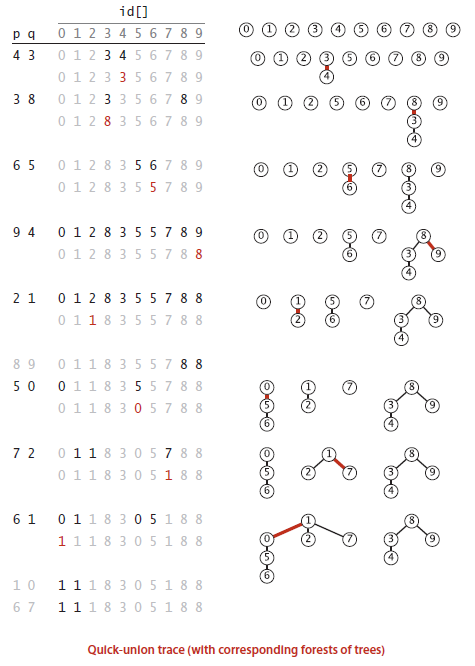
事实上，无论是Quick-Find算法还是Quick-Union算法，他们在图论的基础上基本是起到相互补充的作用。更重要的一点是，我们通过对他们的学习可以认识到，十全十美的算法很难实现，更多的时候算法针对某一个问题的痛点才是有效的。