随机蕨(Random Fern)

最近在做 Zdenek Kalal 的 TLD 算法，其成果发表在CVPR 2010 上，文章的名字叫做 P-N Learning: Bootstrapping Binary Classifiers by Structural Constraints，是关于一个跟踪算法的，主要思想还是实时地对跟踪对象的模型进行更新。检测部分用到了一种作者称为 Fern 的结构，它是在 Random Forests 的基础上改进得到的，不妨称之为Random Fern。下面，根据我的理解和体会总结下 Random Fern 是怎么做的。

　　首先，不得不先说一下论文在进行检测时所使用的特征，是作者定义的一种称之为 2bitBP(2bit Binary Pattern)的特征。

2bitBP(2bit Binary Pattern)的特征

　  这种特征是一种类似于 harr-like 的特征，这种特征包括了特征类型以及相应的特征取值。

假定现在我们要判断一个Patch 块是不是我们要检测的目标。所谓特征类型，就是指在这个 Patch 在 (x,y)坐标，取的一个长 width，高 height 的框子，这个组合 (x, y, width, height) 就是相应的特征类型。

下面解释什么是特征的取值。在已经选定了特征类型的情况下，如果我们把框子左右分成相等的两部分，分别计算左右两部分的灰度和，那么就有两种情况：(1)左边灰度大，(2)右边灰度大，直观的看，就是左右两边哪边颜色更深。同样的，把框子分成上下相等的两部分，也会有两种情况，直观地看，就是上下两边哪边颜色更深。于是在分了上下左右后，总共会有4种情况，可以用 2bit 来描述这4种情况，即可得到相应的特征取值。这个过程可以参见图1。

实际上每种类型的特征都从某个角度来看待我们要跟踪的对象。比如图1中的红框，这个框子中，车灯的地方灰度应该要深一些，那么红框这个类型的特征，实际上就意味着，它认为，如果该 Patch 是一个车子，在相应的地方，相应的长和高，这个地方颜色也应该深一些。

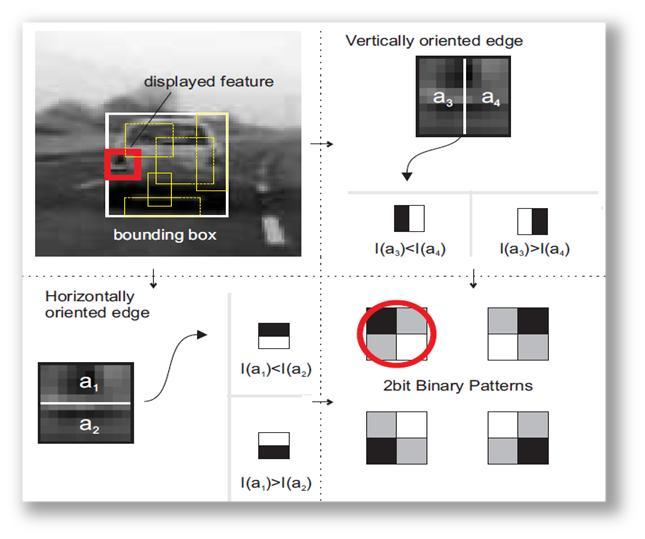
图1. 2bitBP特征说明

接下来，开始介绍 Random Fern。

Random Fern

       前面已经提及，每种类型的特征都代表了一种看待跟踪对象的观点，那么是否可以用若干种类型的特征来进行一个组合，使之更好地描述跟踪的对象呢？答案是肯定的，还是举图1的例子，左边有一个车灯，右边也有一个车灯，如果我们把这两个框子都取到了，可以预见检测的效果会比只有一个框子来得好。Random Fern 的思想就是用多个特征组合来表达对象。

下面，我们先讲一个 Fern 是怎么生成和决策的，再讲多个 Fern 的情况下，如何进行统一决策。

不妨假设我们选定了 nFeat 种类型的特征来表达对象。每个棵 Fern 实际上是一棵4叉树，如图2所示，选了多少种类型的特征，这棵4叉树就有多少层。对于一个 Patch，每一层就用相应的类型的特征去判断，计算出相应类型特征的特征取值，由于采用的是2bitBP特征，会有4种可能取值，在下一层又进行相同的操作，这样每个 Patch 最终会走到最末层的一个叶子节点上。

对于训练过程，要记录落到每个叶子结点上的正样本个数(用nP记)，同时也要记录落到每个叶子结点上的负样本的个数(用nN记)。则可算出正样本落到每个叶子结点上的后验概率nP/(nP+nN)。

对于检测过程，要检测的 Patch 最终会落到某个叶子结点上，由于训练过程已经记录了 正样本落到每个叶子结点上的后验概率，最终可输出该 Patch 为正样本的概率。

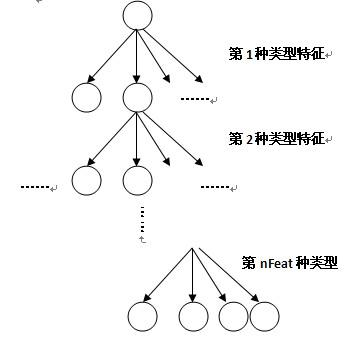
图2. Fern 的结构

前面介绍了一个 Fern 的生成，以及用 Fern 检测一个 Patch，并给出它为正样本的概率。这样多个 Fern进行判断时，就会给出多个后验概率。这就好比我们让多个人来决策，看这个东西是不是正样本，每个人对应于一个 Fern。最终我们计算这一系列的 Fern 输出的后验的均值，看是否大于阈值，从而最终确定它是否是正样本。

补充：

随机蕨分类器（Random Ferns Classifier），类似于随机森林（Random Forest），区别在于随机森林的树中每层节点判断准则不同，而随机蕨的“蕨”中每层只有一种判断准则。

如上图所示，把左面的树每层节点改成相同的判断条件，就变成了右面的蕨。所以蕨也不再是树状结构，而是线性结构。随机蕨分类器根据样本的特征值判断其分类。从图像元中任意选取两点A和B，比较这两点的亮度值，若A的亮度大于B，则特征值为1，否则为0。每选取一对新位置，就是一个新的特征值。蕨的每个节点就是对一对像素点进行比较。

比如取5对点，红色为A，蓝色为B，样本图像经过含有5个节点的蕨，每个节点的结果按顺序排列起来，得到长度为5的二进制序列01011，转化成十进制数字11。这个11就是该样本经过这个蕨得到的结果。

同一类的很多个样本经过同一个蕨，得到了该类结果的分布直方图。高度代表类的先验概率p(F|C)，F代表蕨的结果（如果蕨有s个节点，则共有1+2^s种结果）。

不同类的样本经过同一个蕨，得到不同的先验概率分布。

以上过程可以视为对分类器的训练。当有新的未标签样本加入时，假设它经过这个蕨的结果为00011（即3），然后从已知的分布中寻找后验概率最大的一个。由于样本集固定时，右下角公式的分母是相同的，所以只要找在F=3时高度最大的那一类，就是新样本的分类。

只用一个蕨进行分类会有较大的偶然性。另取5个新的特征值就可以构成新的蕨。用很多个蕨对同一样本分类，投票数最大的类就作为新样本的分类，这样在很大程度上提高了分类器的准确度。