Problem B. Full Binary Tree

题目

链接：http://code.google.com/codejam/contest/2984486/dashboard#s=p1

googlde code jam 2014 Round1A

解题报告下载

word版

归类

动态规划，DFS

解法1[最优解]

耗时

1秒左右

分析

使用DFS和DP。目前为止的最优方案。

关键是用二维数组children_nodes[1001][1001]来表示父节点下的子节点的个数，例如

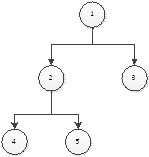
children_nodes[4][2]表示当2节点作为4节点的父亲的时候，4节点极其孩子节点的个数，当然前提是满足full binary tree。

children_nodes[4][2] = 1;

children_nodes[5][2] = 1;

children_nodes[2][1] = 3;

children_nodes[3][1] = 1;

通过children_nodes来记录计算的中间结果，可以大大加速DFS递归。

源码

#include <algorithm>
#include <cstring>
#include <fstream>
#include <iomanip>
#include <iostream>
#include <iterator>
#include <map>
#include <sstream>
#include <string>
#include <vector>

using std::cin;
using std::cout;
using std::endl;
using std::fstream;
using std::map;
using std::stringstream;
using std::string;
using std::vector;

int
get_result(const vector<vector<int> > &_matrix);

int
get_max(const vector<vector<int> > &_matrix, const int _child_row, const int _parent);

int children_nodes[][];

int main(int argc, char *argv[])
{
  int case_amount = ;
  cin >> case_amount;

  for (int i = ; i < case_amount; ++i)
  {
    memset(children_nodes, , sizeof(children_nodes));

    int N = ;
    cin >> N;

    // Step1: Init
    vector<vector<int> > matrix(N + , vector<int>());

    for (int j = ; j < N - ; ++j)
    {
      int row = , column = ;
      cin >> row >> column;

      matrix[row].push_back(column);
      matrix[column].push_back(row);
    }

    const int result = get_result(matrix);
    cout << "Case #" <<  + i << ": " << result << endl;
  }

  return ;
}

int
get_result(const vector<vector<int> > &_matrix)
{
  int max = ;
  for (int i = ; i < _matrix.size(); ++i)
  {
    const int result = get_max(_matrix, i, );

    if (max < result)
      max = result;
  }

  return _matrix.size() - max - ;
}

int
get_max(const vector<vector<int> > &_matrix, const int _child_row, const int _parent)
{
  if ( == children_nodes[_child_row][_parent])
  {
    vector<int> children;

    for (int i = ; i < _matrix[_child_row].size(); ++i)
    {
      if (_parent != _matrix[_child_row][i])
        children.push_back(get_max(_matrix, _matrix[_child_row][i], _child_row));
    }

    std::sort(children.begin(), children.end(), std::greater<int>());

    if (children.size() < )
      children_nodes[_child_row][_parent] = ;
    else
      children_nodes[_child_row][_parent] =  + children[] + children[];
  }

  return children_nodes[_child_row][_parent];
}

解法2[原来递归不会超时]

耗时

20秒左右

分析

使用DFS，深度优先搜索。

实例

Step1:初始化

1	2	3
2	1	4
3	1	7
4	2	5	6
5	4
6	4
7	3

Step2:遍历1-7行

分别计算以每行为root节点的最大节点数；

节点数最多的行，就是root节点，即可得知答案。

源码

#include <algorithm>
#include <fstream>
#include <iomanip>
#include <iostream>
#include <iterator>
#include <map>
#include <sstream>
#include <string>
#include <vector>

using std::cout;
using std::endl;
using std::fstream;
using std::map;
using std::stringstream;
using std::string;
using std::vector;

fstream fs("input.txt", fstream::in);
fstream fout("output.txt", fstream::out);

int
get_int_from_next_line();

string
get_string_from_next_line();

int
get_result(const vector<vector<int> > &_matrix);

int
get_max(const vector<vector<int> > &_matrix, const int _child_row, const int _parent);

int main(int argc, char *argv[])
{
  if (fs.good())
  {
    const int case_amount = get_int_from_next_line();

    for (int i = ; i < case_amount; ++i)
    {
      const int N = get_int_from_next_line();

      // Step1: Init
      vector<vector<int> > matrix(N, vector<int>());

      for (int j = ; j < N - ; ++j)
      {
        const string line = get_string_from_next_line();
        int row = , column = ;
        stringstream temp_stream(line);
        temp_stream >> row >> column;

        matrix[row-].push_back(column-);
        matrix[column-].push_back(row-);
      }

      const int result = get_result(matrix);
      fout << "Case #" <<  + i << ": " << result << endl;
    }
  }

  fs.close();
  fout.close();
  return ;
}

int
get_int_from_next_line()
{
  string line = "";
  getline(fs, line);
  stringstream stream(line);
  int temp = ;
  stream >> temp;
  return temp;
}

string
get_string_from_next_line()
{
  string line = "";
  getline(fs, line);
  return line;
}

int
get_result(const vector<vector<int> > &_matrix)
{
  int max = ;
  for (int i = ; i < _matrix.size(); ++i)
  {
    int result = get_max(_matrix, i, -);

    if (max < result)
      max = result;
  }

  return _matrix.size() - max;
}

int
get_max(const vector<vector<int> > &_matrix, const int _child_row, const int _parent)
{
  vector<int> children;

  for (int i = ; i < _matrix[_child_row].size(); ++i)
  {
    if (_parent != _matrix[_child_row][i])
       children.push_back(get_max(_matrix, _matrix[_child_row][i], _child_row));
   }

  std::sort(children.begin(), children.end(), std::greater<int>());

  if (children.size() < )
    return ;
  else
    return  + children[] + children[];
}

解法3[很笨的方法，自作聪明了]

耗时

3分钟

分析

注意：

题目中给出了Full Binary Tree的定义，只要满足root的每一个子节点有2个或0个子节点。

题目中给出X-Y，说X距离root节点比Y近，没有用。

题目中给出树G没有环。

顶点V与n(n>=3)个点有边

1.    有1,2,3,…,N个顶点，根据输入的关系，初始化二维数组array[N][N]

例如：

1.1    默认初始值为-2

1.2    有边相连，则设置为-1

2    如果N=1直接返回0，N=2直接返回1；如果N>2，则预处理，设row表示第几行，row=0àN-1，即第row节点

如果row行只有一个-1，则继续，否则row++

row节点就是叶子节点，第column列为-1，设置array[row][column]=0，并将与该节点相连的另一个节点，对应的值设置为1，array[column][row]=1

3    设row表示第几行，row=0àN-1，即第row节点

3.0    bool isHasNegtiveOne = false; 表示是否含有-1

3.1    如果row行只有一个-1，则继续，否则跳到3.4；isHasNegtiveOne= true，假设array[row][column]==-1，如果第column行除了第row列没有-1，那么跳到3.2，否则跳到3.3

3.2    如果第column行，除了第row列，非-2的列的数目大于等于2，则

跳到3.2.1，否则跳到3.2.2

3.2.1    在column行选择最大的两列，假设最大两列的和为max，设置array[row][column] = 1 + max；跳到3.3

3.2.2    顶点row作为顶点column的父节点，column节点可以提供1个顶点给row节点，设置array[row][column] = 1；跳到3.3

3.3    如果第row行，除了第column列，非-2的列的数目大于等于2，则跳到3.3.1，否则跳到3.3.2

3.3.1    在row行选择最大的两列，例如下图，最大的两列为4和3，那么顶点column作为顶点row的父节点，row节点可以提供4+3+1个节点给column节点，设置array[column][row] = 8；跳到3.4

-2

4

-1

3

2

3.3.2    顶点column作为顶点row的父节点，row节点可以提供1个顶点给column节点，设置array[column][row] = 1；跳到3.4

3.4    row是否为最后一行，如果不是，则row++继续3.1，如果是，且isHasNegtiveOne为false，则跳到4，否则继续3

4    分别以每一个顶点作为root，计算最大的节点数目

5    删除节点数 = 总结点数 - 最大节点数目

实例

7

4 5    4 2    1 2    3 1    6 4    3 7

Step1:初始化

	1	2	3	4	5	6	7
1	-2	-1	-1	-2	-2	-2	-2
2	-1	-2	-2	-1	-2	-2	-2
3	-1	-2	-2	-2	-2	-2	-1
4	-2	-1	-2	-2	-1	-1	-2
5	-2	-2	-2	-1	-2	-2	-2
6	-2	-2	-2	-1	-2	-2	-2
7	-2	-2	-1	-2	-2	-2	-2

Step2:预处理

对初始的array进行预处理

根据上图，5,6,7行都只有一个-1，例如第5行，存在边（5,4），分别设置array[4][3]=0, array[3][4]=1，即顶点5作为顶点4的孩子只能提供1个节点。

	1	2	3	4	5	6	7
1	-2	-1	-1	-2	-2	-2	-2
2	-1	-2	-2	-1	-2	-2	-2
3	-1	-2	-2	-2	-2	-2	1
4	-2	-1	-2	-2	1	1	-2
5	-2	-2	-2	0	-2	-2	-2
6	-2	-2	-2	0	-2	-2	-2
7	-2	-2	0	-2	-2	-2	-2

Step3: 遍历

根据上图，3,4行只有1个-1，例如第3行，array[2][0] == -1，可推出从顶点1到顶点3，顶点1作为3的父节点，由于顶点3只有一个孩子7，所以顶点3只能提供给顶点1，1个节点，设置array[0][2]=1，同理设置array[1][3]=3。

	1	2	3	4	5	6	7
1	-2	-1	1	-2	-2	-2	-2
2	-1	-2	-2	3	-2	-2	-2
3	-1	-2	-2	-2	-2	-2	1
4	-2	-1	-2	-2	1	1	-2
5	-2	-2	-2	0	-2	-2	-2
6	-2	-2	-2	0	-2	-2	-2
7	-2	-2	0	-2	-2	-2	-2

Step3: 遍历

根据上图，1,2,3,4行只有1个-1，例如第1行，array[0][1] == -1，可推出从顶点2到顶点1，顶点2作为1的父节点，顶点1只有顶点3一个孩子，那么顶点1只能提供顶点2， 1个节点，设置array[1][0]=1，同理设置array[0][1]=1，array[2][0]=1，array[3][1]=1。

	1	2	3	4	5	6	7
1	-2	1	1	-2	-2	-2	-2
2	1	-2	-2	3	-2	-2	-2
3	1	-2	-2	-2	-2	-2	1
4	-2	1	-2	-2	1	1	-2
5	-2	-2	-2	0	-2	-2	-2
6	-2	-2	-2	0	-2	-2	-2
7	-2	-2	0	-2	-2	-2	-2

Step4:

根据上图，每一行都不含有-1，计算每一个顶点作为root节点的最大节点数。

		1	2	3	4	5	6	7
3	1	-2	1	1	-2	-2	-2	-2
5	2	1	-2	-2	3	-2	-2	-2
3	3	1	-2	-2	-2	-2	-2	1
3	4	-2	1	-2	-2	1	1	-2
1	5	-2	-2	-2	0	-2	-2	-2
1	6	-2	-2	-2	0	-2	-2	-2
1	7	-2	-2	0	-2	-2	-2	-2

Step4:

节点2作为root节点，最多有5个节点，去掉2个节点即可。

		1	2	3	4	5	6	7
3	1	-2	1	1	-2	-2	-2	-2
5	2	1	-2	-2	3	-2	-2	-2
3	3	1	-2	-2	-2	-2	-2	1
3	4	-2	1	-2	-2	1	1	-2
1	5	-2	-2	-2	0	-2	-2	-2
1	6	-2	-2	-2	0	-2	-2	-2
1	7	-2	-2	0	-2	-2	-2	-2

源码

#include <algorithm>
#include <fstream>
#include <iomanip>
#include <iostream>
#include <iterator>
#include <map>
#include <sstream>
#include <string>
#include <vector>

using std::cout;
using std::endl;
using std::fstream;
using std::map;
using std::stringstream;
using std::string;
using std::vector;

fstream fs("input.txt", fstream::in);
fstream fout("output.txt", fstream::out);

int
get_int_from_next_line();

string
get_string_from_next_line();

int
get_result(vector<vector<int> > _matrix);

int
get_max_children(const vector<vector<int> > &_matrix, const int _row, const int _column);

int main(int argc, char *argv[])
{
  if (fs.good())
  {
    const int case_amount = get_int_from_next_line();

    for (int i = ; i < case_amount; ++i)
    {
      const int N = get_int_from_next_line();

      // Step1: Init
      vector<vector<int> > matrix(N, vector<int>(N, -));

      for (int j = ; j < N - ; ++j)
      {
        const string line = get_string_from_next_line();
        int row = , column = ;
        stringstream temp_stream(line);
        temp_stream >> row >> column;

        matrix[row-][column-] = -;
        matrix[column-][row-] = -;
      }

      const int result = get_result(matrix);
      fout << "Case #" <<  + i << ": " << result << endl;
    }
  }

  fs.close();
  fout.close();

  return ;
}

int
get_int_from_next_line()
{
  string line = "";
  getline(fs, line);
  stringstream stream(line);
  int temp = ;
  stream >> temp;
  return temp;
}

string
get_string_from_next_line()
{
  string line = "";
  getline(fs, line);
  return line;
}

int
get_result(vector<vector<int> > _matrix)
{
  if ( == _matrix.size())
  {
    return ;
  }
  else if ( == _matrix.size())
  {
    return ;
  }

  // Step2: Preprocess
  for (int row = ; row < _matrix.size(); ++row)
  {
    const int count_not_n2 = _matrix.size() - std::count(_matrix[row].begin(), _matrix[row].end(), -);
    if ( == count_not_n2)
    {
      const vector<int>::const_iterator it = std::find(_matrix[row].begin(), _matrix[row].end(), -);
      const int column = it - _matrix[row].begin();
      _matrix[row][column] = ;
      _matrix[column][row] = ;
    }
  }

  // Step3: loop
  while (true)
  {
    bool isHasNegtiveOne = false;
    for (int row = ; row < _matrix.size(); ++row)
    {
      const int count_1 = std::count(_matrix[row].begin(), _matrix[row].end(), -);
      if ( < count_1)
        isHasNegtiveOne = true;

      if ( == count_1)
      {
        const vector<int>::const_iterator r_it = std::find(_matrix[row].begin(), _matrix[row].end(), -);
        const int column = r_it - _matrix[row].begin();

        // Step: 3.1
        {
          vector<int> column_vec = _matrix[column];
          column_vec.erase(row + column_vec.begin());
          const vector<int>::const_iterator c_it = std::find(column_vec.begin(), column_vec.end(), -);
          if (c_it == column_vec.end())
          {
            // Step: 3.2
            const int column_max_children = get_max_children(_matrix, column, row);
            _matrix[row][column] =  + column_max_children;
          }
        }

        // Step: 3.3
        // column as the parent, row as the child
        // calculate how many nodes can row have
        const int row_max_children = get_max_children(_matrix, row, column);
        _matrix[column][row] =  + row_max_children;
      }
    }

    if (!isHasNegtiveOne)
      break;
  }

  // Step: 4
  int max = ;
  for (int row = ; row < _matrix.size(); ++row)
  {
    std::sort(_matrix[row].begin(), _matrix[row].end(), std::greater<int>());
    int current_max = _matrix[row][] + _matrix[row][];
    if (max < current_max)
      max = current_max;
  }

  return _matrix.size() - max - ;
}

// column as the parent, row as the child
// calculate how many nodes can row have
int
get_max_children(const vector<vector<int> > &_matrix, const int _row, const int _column)
{
  int max_children = ;

  // count of negtive 2
  const int count_n2 = std::count(_matrix[_row].begin(), _matrix[_row].end(), -);
  const int count_not_n2 = _matrix.size() - count_n2;

  if ( >= count_not_n2)
  {
    // Step: 3.3
    max_children = ;
  }
  else
  {
    // Step: 3.2
    // Find the max 2 of _matrix[_row] which can not be _matrix[_row][_column]
    vector<int> m_row = _matrix[_row];
    m_row.erase(_column + m_row.begin());
    std::sort(m_row.begin(), m_row.end(), std::greater<int>());
    max_children = m_row[] + m_row[];
  }

  return max_children;
}

总结

DP+DFS需要1秒；纯DFS需要20秒，我的自作聪明的DP需要3分钟。算法很关键哇！