Python 进制转换、位运算

一、进制转换

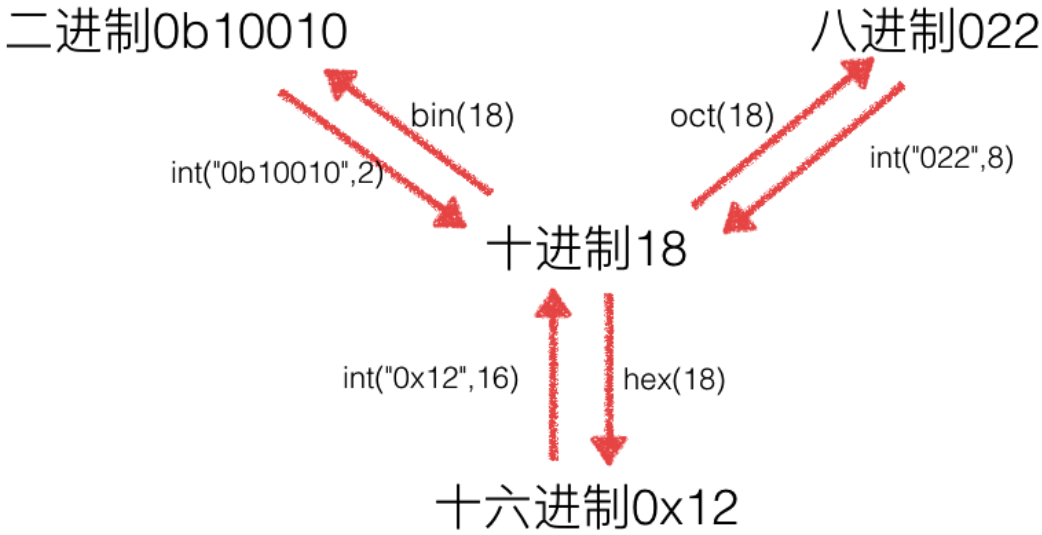
编程用十进制，十进制转换为二进制、八进制、十六进制

In [135]: bin(23)
Out[135]: '0b10111'

In [136]: oct(23)
Out[136]: '0o27'

In [137]: hex(23)
Out[137]: '0x17'

也可以直接反向获取十进制

In [146]: 0b10111
Out[146]: 23

In [147]: 0o27
Out[147]: 23

In [148]: 0x17
Out[148]: 23

也可以用int函数来转换

In [149]: int('0b10111', 2)
Out[149]: 23

In [150]: int('0o27', 8)
Out[150]: 23

In [151]: int('0x17', 16)
Out[151]: 23

---

二、位运算

按位异或的3个特点:
(1) 0^0=0,0^1=1  0异或任何数＝任何数
(2) 1^0=1,1^1=0  1异或任何数－任何数取反
(3) 任何数异或自己＝把自己置0

按位异或的几个常见用途:
(1) 使某些特定的位翻转
    例如对数10100001的第2位和第3位翻转，则可以将该数与00000110进行按位异或运算。
　　　　　  10100001^00000110 = 10100111

(2) 实现两个值的交换，而不必使用临时变量
    例如交换两个整数a=10100001，b=00000110的值，可通过下列语句实现：
　　　　a = a^b； 　　//a=10100111
　　　　b = b^a； 　　//b=10100001
　　　　a = a^b； 　　//a=00000110

---

• & 按位与
• | 按位或
• ^ 按位异或
• ~ 按位取反
• << 按位左移
• >> 按位右移
• 　　用途: 直接操作二进制,省内存,效率高

1)<<按位左移

各二进位全部左移n位,高位丢弃,低位补0

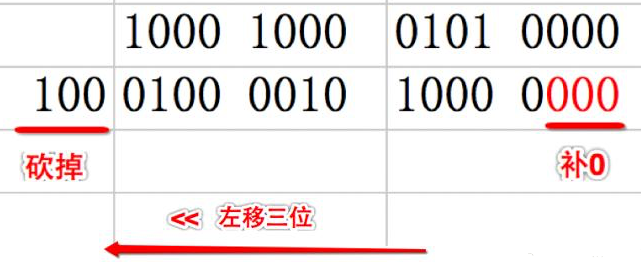
x << n 左移 x 的所有二进制位向左移动n位,移出位删掉,移进的位补零

【注意事项】

• a. 左移1位相当于乘以2
• 用途:快速计算一个数乘以2的n次方 (8<<3 等同于8*2^3)
• b.左移可能会改变一个数的正负性

2)>>右移

各二进位全部右移n位,保持符号位不变
x >> n, x的所有二进制位向右移动n位,移出的位删掉,移进的位补符号位, 右移不会改变一个数的符号

【注意事项】

• 右移1位相当于除以2
• x 右移 n 位就相当于除以2的n次方
• 用途: 快速计算一个数除以2的n次方 (8>>3 等同于8/2^3)

3)& 按位与

全1才1否则0 :只有对应的两个二进位均为1时,结果位才为1,否则为0

4) | 按位或

有1就1 只要对应的二个二进位有一个为1时,结果位就为1,否则为0

5) ^ 按位异或

不同为1 当对应的二进位相异(不相同)时,结果为1,否则为0

6) ~ 取反

~9 = -10

【为什么9取反变成了-10的说明】：

9的原码 ==> 0000 1001 因为正数的原码=反码=补码，所以在 真正存储的时候就是0000 1001

接下来进行对9的补码进行取反操作

进行取反==> 1111 0110 这就是对9 进行了取反之后的补码

既然已经知道了补码，那么接下来只要转换为 咱们人能识别的码型就可以，因此按照规则 ，把这个1111 0110 这个补码 转换为原码即可

符号位不变，其它位取反==> 1000 1001

三、例题

1. 输入一个正数，输出该数二进制表示中1的个数

知识点：把一个整数减去1，再和原整数做与运算，会把该整数最右边一个1变成0。那么一个整数的二进制表示中有多少个1，就可以进行多少次这样的操作。

总结：把一个整数减去1之后再和原来的整数做位与运算，得到的结果相当于是把整数的二进制表示中的最右边一个1变成0 。

代码如下：

def count(n):
    num = 0
    while n:
        n &= (n-1)
        num += 1
    return num

2. 输入两个整数m和n，计算需要改变m的二进制表示中的多少位才能得到n

解决方法：第一步，求这两个数的与或；第二步，统计异或结果中1的位数。

代码如下：

def mton(m,n):
    yihuo = m^n
    count = 0
    while yihuo:
        yihuo &= (yihuo-1)
        count += 1
    print(count) 

3. 用一条语句判断一个整数是不是2的整数次方

解决方法：一个整数如果是2的整数次方，那么它的二进制表示中有且只有一位是1，而其它所有位都是0 。根据前面的分析，把这个整数减去1后再和它自己做与运算，这个整数中唯一的1就变成0了。

代码如下：

def judgebinary(x):
    if x&(x-1) == 0:
        return True
    return False

4.不使用运算符 + 和 - ​​​​​​​，计算两整数 ​​​​​​​a 、b ​​​​​​​之和

 示例：

示例 1:
输入: a = 1, b = 2
输出: 3
示例 2:
输入: a = -2, b = 3
输出: 1

代码如下：

def getSum(a, b):
    """
    :type a: int
    :type b: int
    :rtype: int
    """
    #位操作
    no_carry_sum=a^b #a与b不进位时的和，恰好与异或性质一样
    print(no_carry_sum)
    carry=(a&b)<<1 #a与b的和的进位，恰好是与或操作再左移一位
    print(carry)
    return sum([no_carry_sum,carry])#前两者之和

res = getSum(12,3)
print(res)

总结：两个数的和可以通过将这两个数异或得到这个数不进位时的和，再将这两个数进行与或再左移一位，相当于进位的操作，再将这两个数相加，就可以得到两个数的和

5.判断数字n的二进制数从右往左数第i位是否为1

思路：1<<i可以表示从右向左第i位为1，其余位为0的指示数，

用n与有特定位的指示数与或，就能判断n的特定位是否为1,【长数和短数与或只比较到短数的长度】

举例：10的二进制数倒数第2位是否为1, 10--1010, 1<<1=2--10, 1010&10 = True

代码如下：

def isOne(n,i):
    print(n,1<<i)
    return (n&(1<<i))!=0

res = isOne(10,1)
print(res) #True

　

参考文献：

【1】python中的进制、位运算

【2】深入理解按位异或运算符

【3】java:判断二进制数据中第n位是否为1

【4】Python3.X中的位运算符