nginx学习时使用EditPuls编辑conf.xml
一、Nginx简介:是一个使用c语言开发的高性能的http服务器及反向代理服务器
二、由于在linux环境中使用vim修改配置文件相对困难。为此,我们可以借助EditPlus将虚拟机上面的目录引用到EditPlus编辑器中,使得编辑相关文件(vim文件)更加方便。具体步骤如下:
1、 点击左上角的File-FTP-FTPSettings
2、 按下图的步骤进行操作
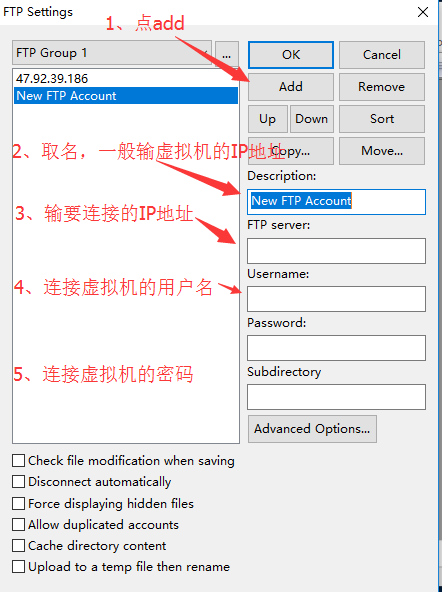
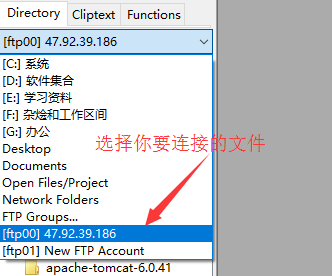
3、完成上面的操作后,按照下图进行操作

3、选择你要连接的文件
nginx学习时使用EditPuls编辑conf.xml的更多相关文章
- [转帖]nginx学习,看这一篇就够了:下载、安装。使用:正向代理、反向代理、负载均衡。常用命令和配置文件
nginx学习,看这一篇就够了:下载.安装.使用:正向代理.反向代理.负载均衡.常用命令和配置文件 2019-10-09 15:53:47 冯insist 阅读数 7285 文章标签: nginx学习 ...
- Nginx学习一路向西
Nginx 学习一路向北 Java大猿帅成长手册,GitHub JavaEgg ,N线互联网开发必备技能兵器谱 1. Nginx简介 1.1 Nginx 概述 NGINX是一个免费.开源.高性能.轻量 ...
- nginx学习,看这一篇就够了:下载、安装。使用:正向代理、反向代理、负载均衡。常用命令和配置文件
前言一.nginx简介1. 什么是 nginx 和可以做什么事情Nginx 是高性能的 HTTP 和反向代理的web服务器,处理高并发能力是十分强大的,能经受高负 载的考验,有报告表明能支持高达 50 ...
- Nginx学习之配置RTMP模块搭建推流服务
写在开始 小程序升级实时音视频录制及播放能力,开放 Wi-Fi.NFC(HCE) 等硬件连接功能.同时提供按需加载.自定义组件和更多访问层级等新特性,增强了第三方平台的能力,以满足日趋丰富的业务需求. ...
- Nginx学习系列二Linux下Nginx实现负载均衡
关于在本地虚拟机(VMware 14)下安装Linux同时安装Nginx,请参考Nginx学习系列之搭建环境 1.启动Nginx 在Nginx安装成功的前提下,启动Nginx 已root模式登陆(权限 ...
- Nginx系列0:Nginx学习历程
Nginx学习历程 一.初识Nginx 1.Nginx适用于哪些场景 (1)静态资源服务 通过本地文件系统提供服务 (2)反向代理服务 Nginx的强大性能 缓存 负载均衡 (3)API服务 Open ...
- nginx 学习笔记(2) nginx新手入门
这篇手册简单介绍了nginx,并提供了一些可以操作的简单的工作.前提是nginx已经被安装到你的服务器上.如果没有安装,请阅读上篇:nginx 学习笔记(1) nginx安装.这篇手册主要内容:1. ...
- Nginx学习之从零搭建静态资源网站
前言 在某学习网站学习了nginx的安装和使用,以此文记录. 环境准备 安装在VMWare下的Centos虚拟机.由于我这是新装的虚拟机.所以很多插件都没有,这里干脆一次性安装上. wget ...
- Nginx学习笔记之加强篇
在上一篇文章Nginx学习笔记之应用篇中,我们已经可以正式运行自己的网站了.但是在使用Nginx服务器时还需要注意几个问题: 1.Nginx服务器上配置的单个站点的并发量不超过1024 2.Nginx ...
随机推荐
- SPOJ - PHRASES
题意: 给n个字符串,求出最长的子串.使得子串在每个字符串中不重叠地至少出现2次.输出子串长度. 题解: 用后缀数组求出height数组,之后二分答案.check时对height数组进行分组,并维护每 ...
- CF449C:Jzzhu and Apples——题解
https://vjudge.net/problem/CodeForces-449C 题目大意:1-n编号的苹果两两一对,他们的最大公约数不为1,求这些对的最大匹配. ———————————————— ...
- 字符串构造的dp 【bzoj1009 &bzoj1030】
1009: [HNOI2008]GT考试 Time Limit: 1 Sec Memory Limit: 162 MB Submit: 4305 Solved: 2637 [Submit][Sta ...
- [POI2014]DOO-Around the world
通过几年的努力,Byteasar最终拿到了飞行员驾驶证.为了庆祝这一事实,他打算买一架飞机并且绕Byteotia星球赤道飞行一圈.但不幸的是赤道非常长所以需要中途加几次油.现在已知赤道上面所有飞机场, ...
- 用JQuery实现自定义选择桌面
有些时候,我们可以为用户提供很贴心的功能,比如判断用户是什么时候来访问的,然后给出一句问候,晚上好,下午好之类的.并且更换网页的背景颜色,比如晚上的时候就可以用满天星星的背景,白天就用阳光灿烂,或者特 ...
- Codeforces Round #341 (Div. 2)B
B. Wet Shark and Bishops time limit per test 2 seconds memory limit per test 256 megabytes input sta ...
- 打开cmd窗口新技巧get
1.在当前目录下,按住shift键+点击右键,选择在此处打开命令窗口 很多时候我们需要打开命令行然后进入到相应目录进行一些操作. 常规的做法是: Win+R打开运行窗口 输入"cmd&quo ...
- wamp环境介绍
一.简介 Wamp就是 Windows Apache Mysql PHP集成安装环境,即在window下的apache.php和mysql的服务器软件. 二.常用的集成环境 XAMPP - XAMPP ...
- [LeetCode] 接雨水,题 Trapping Rain Water
这题放上来是因为自己第一回见到这种题,觉得它好玩儿 =) Trapping Rain Water Given n non-negative integers representing an eleva ...
- HDU 5901 Count primes 大素数计数
题意:计算1~N间素数的个数(N<=1e11) 题解:题目要求很简单,作为论文题,模板有两种 \(O(n^\frac{3}{4} )\),另一种lehmer\(O(n^\frac{2}{3})\ ...
