【BZOJ】2017: [Usaco2009 Nov]硬币游戏（dp+神题+博弈论）

http://www.lydsy.com/JudgeOnline/problem.php?id=2017

这题太神了，我想了一个中午啊

原来是看错题一直没理解题解说的，一直以为题解是错的QAQ

“开始玩游戏时，第一个玩家可以从堆顶拿走一枚或两枚硬币”

果然还是太弱

我们发现，每一个阶段都由上一个玩家决定的，即别人怎么拿限制了我怎么拿，那么

设状态为f(i, j)表示剩余i个硬币，上次拿了j个硬币，注意，是上一次！

则

f(i, j)=max{sum(1, i)-f(i-k, k)} 1<=k<=2*j

这点可以参照前边一题的dp博弈

sum(1, i)包含了2重意思，即sum(1, i-k), sum(i-k+1, i)，前者是之前局面的和，后者是玩家所得的价值

而f(i-k, k)的意思就是根据上一次所拿硬币j限制了我这次拿硬币k，而这个状态就表示我这次拿了k个之后还剩与i-k个，而且是从我这个状态k个限制了它所拿硬币。

然后注意读入是倒序即可

但是这样做状态是n^2，转移n，显然2000的数据tle。

那么我们要优化

（以下优化转自http://hi.baidu.com/tankche1/item/dda6af9b68f301c5b7253190

我们来看看f(10,1)的情况。

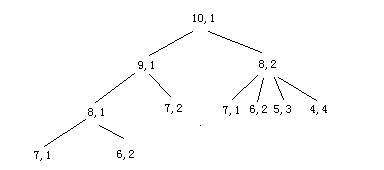
在这里，我们发现f(8,2)和f(8,1)的区别就是比其多了2条路，所以我们完全能想到以下方法。

将除了自己特有的两条路保留后，另两条路舍去，直接连到f(8,1)的最优解上，这样就能将时间复杂度优化为O(n^2)，这样的话，我们的状态转移方程可以写为f(x,y)=Max{ f(x,y-1),sum[x]-Min{f(x-(2*y-1),2*y-1),f(x-2*y,2*y)} }

#include <cstdio>

#include <cstring>

#include <cmath>

#include <string>

#include <iostream>

#include <algorithm>

#include <queue>

using namespace std;

#define rep(i, n) for(int i=0; i<(n); ++i)

#define for1(i,a,n) for(int i=(a);i<=(n);++i)

#define for2(i,a,n) for(int i=(a);i<(n);++i)

#define for3(i,a,n) for(int i=(a);i>=(n);--i)

#define for4(i,a,n) for(int i=(a);i>(n);--i)

#define CC(i,a) memset(i,a,sizeof(i))

#define read(a) a=getint()

#define print(a) printf("%d", a)

#define dbg(x) cout << #x << " = " << x << endl

#define printarr(a, n, m) rep(aaa, n) { rep(bbb, m) cout << a[aaa][bbb]; cout << endl; }

inline const int getint() { int r=0, k=1; char c=getchar(); for(; c<'0'||c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) r=r*10+c-'0'; return k*r; }

inline const int max(const int &a, const int &b) { return a>b?a:b; }

inline const int min(const int &a, const int &b) { return a<b?a:b; }

const int N=2005;

int f[N][N], n, a[N], sum[N];

int main() {

	read(n);

	for3(i, n, 1) read(a[i]);

	for1(i, 1, n) sum[i]=sum[i-1]+a[i];

	for1(i, 1, n)

		for1(j, 1, n) {

			f[i][j]=f[i][j-1];

			if(i>=(j<<1))

				f[i][j]=max(f[i][j], sum[i]-f[i-(j<<1)][(j<<1)]);

			if(i-((j<<1)-1)>=0)

				f[i][j]=max(f[i][j], sum[i]-f[i-((j<<1)-1)][(j<<1)-1]);

		}

	print(f[n][1]);

	return 0;

}

Description

农夫约翰的奶牛喜欢玩硬币游戏，因此他发明了一种称为“Xoinc”的两人硬币游戏。初始时，一个有N(5 <= N <= 2,000)枚硬币的堆栈放在地上，从堆顶数起的第I枚硬币的币值为C_i (1 <= C_i <= 100,000)。开始玩游戏时，第一个玩家可以从堆顶拿走一枚或两枚硬币。如果第一个玩家只拿走堆顶的一枚硬币，那么第二个玩家可以拿走随后的一枚或两枚硬币。如果第一个玩家拿走两枚硬币，则第二个玩家可以拿走1，2，3，或4枚硬币。在每一轮中，当前的玩家至少拿走一枚硬币，至多拿走对手上一次所拿硬币数量的两倍。当没有硬币可拿时，游戏结束。两个玩家都希望拿到最多钱数的硬币。请问，当游戏结束时，第一个玩家最多能拿多少钱呢？

Input

第1行：1个整数N

第2..N+1行：第i+1行包含1个整数C_i

Output

第1行：1个整数表示第1个玩家能拿走的最大钱数。

Sample Input

5
1
3
1
7
2

Sample Output

HINT

样例说明：第1个玩家先取走第1枚，第2个玩家取第2枚；第1个取走第3，4两枚，第2个玩家取走最后1枚。

Source

Silver