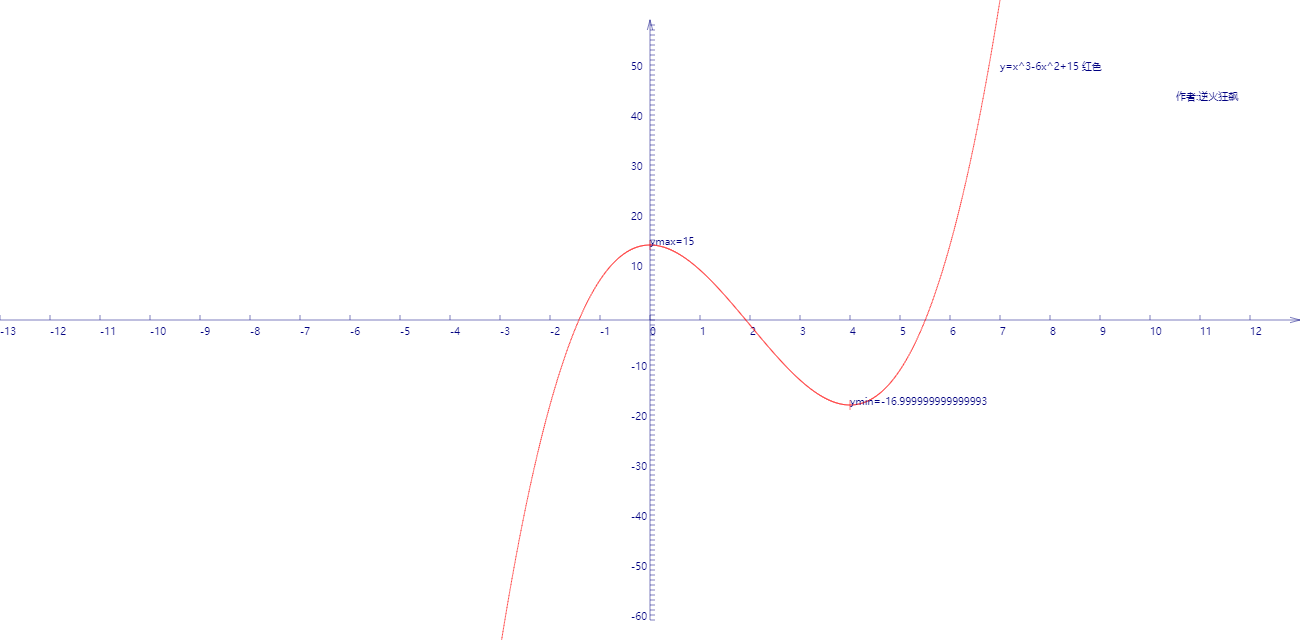
求x>0时,y=x^3-6x^2+15的极值
解:
当x→∞时,y也→∞,所以y没有最大值。
y=x3-6x2+15=-4*(x/2)*(x/2)*(6-x)+15
而根据几何平均数小于等于算术平均数的定理,(x/2)*(x/2)*(6-x)在x/2=6-x时取得最大值,同时y取得最小值。
而x/2=6-x可以得出x=4,此时ymin=16*(-2)+15=-17
上述结果的正确性可以用微分验证,当y的导数y'=3x2-12x=0时,y有极值。
而3x2-12x=0也可以得出x=4.
下图可以直观看出y=x3-6x2+15的极值
曲线:
代码:
<!DOCTYPE html>
<html lang="utf-8">
<meta http-equiv="Content-Type" content="text/html; charset=utf-8"/>
<head>
<title>绘制函数y=x^3-6x^2+15曲线</title>
</head>
<body onload="draw()">
<canvas id="myCanvus" width="1300px" height="640px" style="border:1px dashed black;">
出现文字表示你的浏览器不支持HTML5
</canvas>
</body>
</html>
<script type="text/javascript">
<!--
function draw(){
var canvas=document.getElementById("myCanvus");
var canvasWidth=1300;
var canvasHeight=640;
var context=canvas.getContext("2d");
context.fillStyle = "white";
context.fillRect(0, 0, canvasWidth, canvasHeight);
context.strokeStyle = "black";
context.fillStyle = "black";
// 进行坐标变换:把原点放在左下角,东方为X轴正向,北方为Y轴正向
var offsetY=320;// Y向偏移值,正值向上偏,用来画坐标轴
var offsetX=650;// X向偏移值,正值向右偏,用来画坐标轴
context.save();
context.translate(0+offsetX,canvasHeight-offsetY);
drawAxisXText(context);// 文字和线分开画比较好处理
drawAxisYText(context);
drawTitleText(context);
context.rotate(getRad(180));
context.scale(-1,1);
drawAxisX(context);
drawAxisY(context);
drawCurve(context);
context.restore();
}
function drawTitleText(ctx){
ctx.lineWidth=0.5;
ctx.strokeStyle='navy';
ctx.fillStyle='navy';
var x=350;
var y=-250;
// 写文字
ctx.fillText("y=x^3-6x^2+15 红色",x,y);
//ctx.fillText("y=x*x-4*x+4 绿色",x,y+20);
//ctx.fillText("y=x*x 黄色",x,y+40);
//ctx.fillText("y=x*x+4*x+5 青柠色",x,y+60);
//ctx.fillText("y=-(x*x-7*x+12)/5 紫色",x,y+80);
//ctx.fillText("y=-(x*x+2*x+2)*4 栗色",x,y+100);
ctx.fillText(" 作者:逆火狂飙",x+170,y+30);
}
function drawCurve(ctx){
var cds=[{}];
var cds1=[{}];
var cds2=[{}];
var cds3=[{}];
var cds4=[{}];
var cds5=[{}];
var cds6=[{}];
var ymax=-1000,ymin=1000,xmax,xmin;
var x,y;
for(x=-13;x<=13;x+=0.01){
y=Math.pow(x,3)-6*Math.pow(x,2)+15;//
var arr={"x":x,"y":y};
cds.push(arr);
}
paintCurve(ctx,"red",cds);
for(var i=0; i<cds.length; i++){
// 求y最大值
if(cds[i].x<0 && cds[i].y>ymax){
ymax=cds[i].y;
xmax=cds[i].x;
}
// 求y最小值
if(cds[i].x>=0 && cds[i].y<ymin){
ymin=cds[i].y;
xmin=cds[i].x;
}
}
console.log("ymin="+ymin+" xmin="+xmin+" ymax="+ymax+" ymin="+ymin+" xmax="+xmax);
var SU=50;// Scale Unit
// 极大值
ctx.beginPath();
ctx.moveTo(xmax*SU,ymax*5-5);
ctx.lineTo(xmax*SU,ymax*5+5);
ctx.save();
ctx.scale(1,-1);
ctx.fillText("ymax="+cutShort(ymax.toString(),8),xmax*SU,-ymax*5);
ctx.restore();
ctx.stroke();
ctx.closePath();
// 极小值
ctx.beginPath();
ctx.moveTo(xmin*SU,ymin*5-5);
ctx.lineTo(xmin*SU,ymin*5+5);
ctx.save();
ctx.scale(1,-1);
ctx.fillText("ymin="+ymin,xmin*SU,-ymin*5);
ctx.restore();
ctx.stroke();
ctx.closePath();
/*paintCurve(ctx,"green",cds1);
paintCurve(ctx,"yellow",cds2);
paintCurve(ctx,"lime",cds3);
paintCurve(ctx,"purple",cds4);
paintCurve(ctx,"maroon",cds5);*/
//paintCurve(ctx,"maroon",cds6);*/
}
function paintCurve(ctx,color,cds){
var SU=50;// Scale Unit
ctx.strokeStyle = color;
ctx.beginPath();
for(var i=0; i<cds.length; i++){
ctx.lineTo(cds[i].x*SU,cds[i].y*5);// 注意y轴比例
}
ctx.stroke();
ctx.closePath();
}
function drawAxisX(ctx){
ctx.save();
ctx.lineWidth=0.5;
ctx.strokeStyle='navy';
ctx.fillStyle='navy';
var start=-650;
var end=650;
// 画轴
ctx.beginPath();
ctx.moveTo(start, 0);
ctx.lineTo(end, 0);
ctx.stroke();
ctx.closePath();
// 画箭头
ctx.beginPath();
ctx.moveTo(end-Math.cos(getRad(15))*10, Math.sin(getRad(15))*10);
ctx.lineTo(end, 0);
ctx.lineTo(end-Math.cos(getRad(15))*10, -Math.sin(getRad(15))*10);
ctx.stroke();
ctx.closePath();
// 画刻度
var x,y;
y=5;
for(x=start;x<end;x+=50){
ctx.beginPath();
ctx.moveTo(x, 0);
ctx.lineTo(x, y);
ctx.stroke();
ctx.closePath();
}
ctx.restore();
}
function drawAxisXText(ctx){
ctx.lineWidth=0.5;
ctx.strokeStyle='navy';
ctx.fillStyle='navy';
var start=-650;
var end=650;
// 写文字
var x,y=5;
for(x=start;x<end;x+=50){
ctx.fillText(x/50,x,y+10);
}
}
function drawAxisY(ctx){
ctx.save();
ctx.lineWidth=0.5;
ctx.strokeStyle='navy';
ctx.fillStyle='navy';
var start=-300;
var end=300;
// 画轴
ctx.beginPath();
ctx.moveTo(0, start);
ctx.lineTo(0, end);
ctx.stroke();
ctx.closePath();
// 画箭头
ctx.beginPath();
ctx.moveTo(Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
ctx.lineTo(0, end);
ctx.lineTo(-Math.sin(getRad(15))*10, end-Math.cos(getRad(15))*10);
ctx.stroke();
ctx.closePath();
// 画刻度
var x,y;
x=5;
for(y=start;y<end;y+=5){// 注意y轴比例
ctx.beginPath();
ctx.moveTo(x, y);
ctx.lineTo(0, y);
ctx.stroke();
ctx.closePath();
}
}
function drawAxisYText(ctx){
ctx.lineWidth=0.5;
ctx.strokeStyle='navy';
ctx.fillStyle='navy';
var start=-250;
var end=350;
// 写文字
var x=-19,y=5;
for(y=start;y<end;y+=50){
if(y!=0){
ctx.fillText(-y/5,x,y);// 注意y轴比例
}
}
}
function getRad(degree){
return degree/180*Math.PI;
}
function cutShort(str,length){
if(str.length>length){
str=str.substr(0,length)+"...";
}
return str;
}
//-->
</script>
求x>0时,y=x^3-6x^2+15的极值的更多相关文章
- 求x>0时,y=x^3-6x^2+15的极值
解: 当x→∞时,y也→∞,所以y没有最大值. y=x3-6x2+15=-4*(x/2)*(x/2)*(6-x)+15 而根据几何平均数小于等于算术平均数的定理,(x/2)*(x/2)*(6-x)在x ...
- chart.js插件生成折线图时数据普遍较大时Y轴数据不从0开始的解决办法[bubuko.com]
chart.js插件生成折线图时数据普遍较大时Y轴数据不从0开始的解决办法,原文:http://bubuko.com/infodetail-328671.html 默认情况下如下图 Y轴并不是从0开始 ...
- 2017-12-15python全栈9期第二天第七节之x or y ,x 为 非 0时,则返回x
#!/user/bin/python# -*- coding:utf-8 -*-# x or y ,x 为 非 0时,则返回xprint(1 or 2)print(3 or 2)print(0 or ...
- 编写一函数用来实现左右循环移位。函数原型为move(value,n);n>0时右移n位,n<0时左移|n|位。
#include<stdio.h> #include<stdlib.h> int main(){ setbuf(stdout,NULL); int move(int,int); ...
- 给定n,求1/x + 1/y = 1/n (x<=y)的解数~hdu-1299~(分解素因子详解)
链接:https://www.nowcoder.com/acm/contest/90/F来源:牛客网 题目描述 给定n,求1/x + 1/y = 1/n (x<=y)的解数.(x.y.n均为正整 ...
- MySQL relay_log_purge=0 时的风险
转自: http://xiezhenye.com/2015/12/mysql-relay_log_purge0-%E6%97%B6%E7%9A%84%E9%A3%8E%E9%99%A9.html 有时 ...
- .net4.0切换2.0时,SplitContainer”的对象强制转换为类型
问 题:将dotnet framework 4.0 切换到2.0时,编译没有问题,在运行时出现如下错误:System.InvalidCastException: 无法将类型为“System.Windo ...
- mybatis查询参数为0时无法识别问题
最近在工作中遇到一个mybatis参数问题,主要是列表查询按照状态进行过滤,其中已完成状态值是0,被退回是1.如图所示 , 然后Mapper里面是和平常一样的写法<if test="s ...
- Shell脚本中字符串判空:使用-z 字符串长度为0时,为真,-n字符串长度不为0,为真。这两个都不靠谱【转】
最近发现使用 -z 和 -n 来判断字符串判空,或不空时,很不靠谱. 使用下面的方法最可靠: if [ "x${value}" == "x" ] ...
随机推荐
- sublime text3 自己定义的不同浏览器的预览快捷键
sublime text3 自己定义的不同浏览器的预览快捷键突然全部失效了,搞到现在一直没闹清楚怎么回事,翻看插件发现SideBarEnhancements这插件刚更新了,快捷键也是依赖这个插件弄得. ...
- Nmap误报1720端口开放的原因
在使用Nmap扫描服务器开放端口(全连接扫描)时,一直会发现误报1720端口开放,telnet也有时会连接成功.而实际上服务器并未开启此端口.经过查阅资料,确定原因如下: H.323协议在负载中放入了 ...
- PHP 边执行边输出
<?php for ($i = 1; $i <= 5; $i++) { print "#$i 完毕<hr>"; sleep(1); print str_pa ...
- BZOJ 4873 寿司餐厅(最大权闭合图 网络流)
寿司餐厅 时间限制: 1 Sec 内存限制: 512 MB提交: 6 解决: 3[提交][状态][讨论版] 题目描述 Kiana 最近喜欢到一家非常美味的寿司餐厅用餐.每天晚上,这家餐厅都会按顺序 ...
- 简单了解gzip、bzip2、xz
压缩工具gzip.bzip2.xz分别对应压缩格式.gz..bz2..xz.不过tar命令已经可以满足大部分使用,所以这些格式只简单了解一下.gzip压缩速度最快,xz压缩率最高,bz2适中.一般这三 ...
- Abp数据库迁移注意事项
前记:昨天下载了一个Abp模板,然后尝试利用EF CodeFirst进行数据库生成操作,然后就是一直报错 在与 SQL Server 建立连接时出现与网络相关的或特定于实例的错误.未找到或无法访问服务 ...
- 课堂作业-Bag类的实现
课堂作业-Bag类的实现 要求: 代码运行在命令行中,路径要体现学号信息,IDEA中,伪代码要体现个人学号信息 参见Bag的UML图,用Java继承BagInterface实现泛型类Bag,并对方法进 ...
- android 关于Make sure the plugin is properly configured问题的解决办法
这个问题引发的原因最初的报错是: [2013-10-14 10:01:58 - XXX] The connection to adb is down, and a severe error has o ...
- OPENCV下SIFT算法使用方法笔记
这几天继续在看Lowe大神的SIFT神作,看的眼花手脚抽筋.也是醉了!!!!实在看不下去,来点干货.我们知道opencv下自带SIFT特征检测以及MATCH匹配的库,这些库完全可以让我们进行傻瓜似的操 ...
- WPF中的动画——(二)From/To/By 动画
我们所实现的的动画中,很大一部分是让一个属性在起始值和结束值之间变化,例如,我在前文中实现的改变宽度的动画: var widthAnimation = new DoubleAnimation() ...
