FIR滤波器相关解释

---

LTI（Linear Time-Invariant）

线性时不变：

线性时不变系统是根据系统输入和输出是否具有线性关系来定义的。满足叠加原理的系统具有线性特性。线性满足y=kx函数。

根据系统的输入和输出关系是否具有线性来定义 满足叠加原理的系统具有线性特性。即若对两个激励x1(n)和x2(n)，有T[ax1(n)+bx2(n)]=aT[x1(n)]+bT[x2(n)]，式中a、b为任意常数。

时不变系统

时不变系统：就是系统的参数不随时间而变化，即不管输入信号作用的时间先后，输出信号响应的形状均相同，仅是输入信号出现的时间不同。用数学表示为T[x(n)]=y[n]则 T[x(n-n0)]=y[n-n0]，这说明序列x(n)先移位后进行变换与它先进行变换后再移位是等效的。

线性时不变系统

线性时不变系统：既满足叠加原理又具有时不变特性，它可以用单位脉冲响应来表示。单位脉冲响应是输入端为单位脉冲序列时的系统输出，一般表示为h(n)，即h(n)=T[δ(n)]。

任一输入序列x(n)的响应y(n)=T[x(n)]=T[ δ(n-k)]；

由于系统是线性的，所以上式可以写成y(n)=T[δ(n-k)]；

又由于系统是时不变的，即有T[δ(n-k)]=h(n-k)；

从而得y(n)=h(n-k)=x(n)*h(n)；

这个公式称为线性卷积，用“*”表示。

齐次性

若激励f(t)产生的响应为y(t)，则激励Af(t)产生的响应即为Ay(t)，此性质即为齐次性。其中A为任意常数。

f(t)系统y(t)，Af(t)系统Ay(t)

叠加性

若激励f1(t)与f2(t)产生的响应分别为y1(t)， y2(t)，则激励f1(t)+f2(t)产生的响

应即为y1(t)+y2(t)，此性质称为叠加性。

线性

若激励f1(t)与f2(t)产生的响应分别为y1(t)， y2(t)，则激励A1f1(t)+A2f2(t)产生的响应即为A1y1(t)+A2y2(t)，此性质称为线性。

时不变性

若激励f(t)产生的响应为y(t)，则激励f(t-t0)产生的响应即为y(t-t0)，此性质称为不变性，也称定常性或延迟性。它说明，当激励f(t)延迟时间t0时，其响应y(t)也延迟时间t0，且波形不变。

微分性

若激励f(t)产生的响应为y(t)，则激励f'(t)产生的响应即y’(t),此性质即为微分性。

积分性

若激励f(t)产生的响应为y(t)，则激励f(t)的积分产生的响应即为y(t)的积分。此性质称为积分性。

---

FIR滤波器结构：

直接形式的FIR滤波器

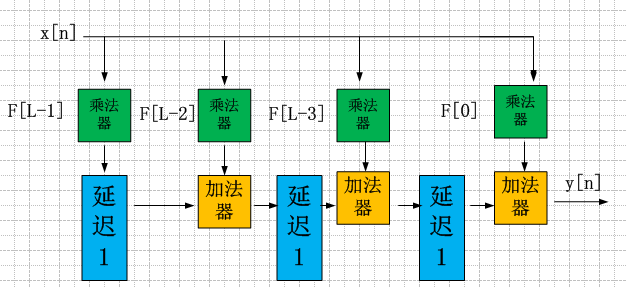
转置结构的FIR滤波器

---

FIR滤波器特点：

• • FIR滤波器的最主要的特点是没有反馈回路，稳定性强，故不存在不稳定的问题；

  • FIR具有严格的线性相位，幅度特性随意设置的同时，保证精确的线性相位;

  • 设计方式是线性的，硬件容易实现；

  • 滤波器过度工程有有限区间；

  • FIR滤波器设计需要更多的参数，增加计算量

---

版权所有权归卿萃科技 杭州FPGA事业部，转载请注明出处

作者：杭州卿萃科技ALIFPGA

原文地址：杭州卿萃科技FPGA极客空间 微信公众号

---

扫描二维码关注杭州卿萃科技FPGA极客空间

---