#510. 「LibreOJ NOI Round #1」动态几何问题

---

题目:

题解:

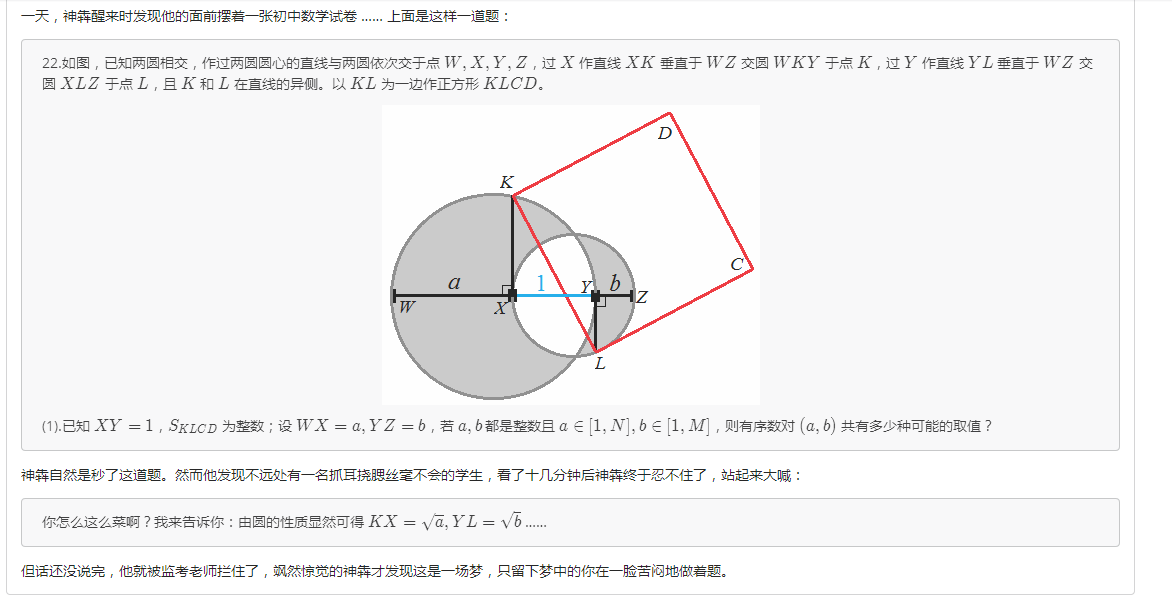
几何部分,先证明一下 \(KX = \sqrt{a},YL = \sqrt{b}\)

设左侧的圆心为 \(O\) ,连接 \(OK\) ,我们有 \(OK = r\).

然后有 \(r = \frac{a+1}{2},OX = r - a\)

勾股定理有 : \(KX^2 = OK^2 + OX^2\) 解得 : \(KX = \sqrt{a}\).

同理 : \(YL = \sqrt{b}\).

然后我们将 \(YL\) 向左平移直到 \(b\) 与 \(X\) 重合,设此时点 \(L\) 所在处为 \(N\).

那么有 : \(KN^2 + NL^2\) 是整数.

整理可得 : \(\sqrt{ab}\) 是整数.

那么现在的问题就是问有多少有序数对 \((a,b)\) 满足 \(a \in [1,n],b \in [1,m] 且 \sqrt{ab} 是整数\)

对于 \(a\) 这个数字，我们考虑把它拆开 : 令 \(a = a_1^2*a_2\)

其中 \(a_2\) 不含平方因子.

对于 \(b_2\) 同样的拆成 \(b = b_1^2*b_2\)

那么我们发现原来的式子变成了 \(a_1b_1\sqrt{a_2b_2}\)

因为两个不含平方因子的数的乘积变成一个完全平方数，所以易得 \(a_2 = b_2\) , 设为 \(d\).

所以我们可以枚举 \(1\space .. n\) 的 \(d\) ，只要我们保证 \(d\) 不含平方因子即可.

那么对于一个确定的 \(d\) ,由于我们知道 \(d*a_1^2 \leq n\)所以有 \(a_1^2 \leq \lfloor \frac{n}{d}\rfloor\)

那么我们知道对于 \(n\) 以内的完全平方数一共有 \(\lfloor \sqrt{n} \rfloor\) 个。

那么我们就知道对于一个确定的 \(d\) ,有 \(\lfloor \sqrt{\lfloor \frac{n}{d}\rfloor}\rfloor\) 个满足条件的 \(a\)。

那么我们发现计算式实际上就是 :

\[\sum_{i=1}^{min(n,m)}\mu(i)^2 \lfloor \sqrt{\lfloor \frac{n}{d}\rfloor}\rfloor \lfloor \sqrt{\lfloor \frac{m}{d}\rfloor}\rfloor
\]

然后我们考虑如何计算 \(\mu(i)^2\).

我们通过意义来考虑，这实际上就是对是质因子平方倍数的数逐个筛去。

考虑容斥原理，然后用 \(\mu(i)\) 做容斥系数。

我们发现有 : \(\sum_{i=1}^n\mu(i)^2 = \sum_{i=1}^{\sqrt{n}}\mu(i)\lfloor \frac{n}{i^2}\rfloor\)

我们可以提前线性筛出前 \(\sqrt{n}\) 的 \(\mu\) ,然后对于后面的 \(\sum\) 式我们跳块求就好了.

可以证明 : \(\lfloor \frac{n}{i^2} \rfloor\) 的不同值的数目不超过 \(O(n^{\frac{1}{3}})\).

然后计算主计算式的时候后面的两部分也跳块就好了。

常数优越即 \(AC\) ,否则 \(95\).

#include <map>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
inline void read(ll &x){
	x=0;static char ch;static bool flag;flag = false;
	while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
	while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
#define rg register int
#define rep(i,a,b) for(rg i=(a);i<=(b);++i)
#define per(i,a,b) for(rg i=(a);i>=(b);--i)
const int maxn = 124000000;
int pri[maxn/10],f[maxn],cnt,sqrn;
short mu[maxn];bool vis[maxn];
inline void liner(int n){
	mu[1] = f[1] = 1;
	rep(i,2,n){
		if(!vis[i]){
			pri[++cnt] = i;
			mu[i] = -1;
		}
		rep(j,1,cnt){
			ll x = 1LL*i*pri[j];
			if(x > n) break;
			vis[x] = true;
			if(i % pri[j] == 0) break;
			mu[x] = -mu[i];
		}
		f[i] = mu[i]*mu[i];
		mu[i] += mu[i-1];
		f[i] += f[i-1];
	}
}
map<ll,ll>g;
inline ll mu_2(ll n){
	if(n <= sqrn) return f[n];
	if(g.count(n)) return g[n];
	ll res = 0,i = 1;
	for(;i*i*i<=n;++i) res += n/(i*i)*(mu[i] - mu[i-1]);
	for(ll j,v;i*i <= n;i = j+1){
		j = sqrt(n / (v = (n / (i*i))) );
		res += (mu[j] - mu[i-1])*v;
	}return g[n] = res;
}
int main(){
	ll n,m;read(n);read(m);
	if(n > m) swap(n,m);
	liner(sqrn = sqrt(n));
	ll ans = 0,la = 0,tmp;
	for(ll i = 1,j,v1,v2;i <= n; i = j+1){
		v1 = sqrt(n / i);v2 = sqrt(m / i);
		j = min(n / (v1*v1),m / (v2*v2));
		ans += ((tmp = mu_2(j)) - la)*v1*v2;
		la = tmp;
	}printf("%lld\n",ans);
	return 0;
}