HihoCoder 1122二分图二 ---最大匹配之匈牙利算法

二分图二•二分图最大匹配之匈牙利算法

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

上一回我们已经将所有有问题的相亲情况表剔除了，那么接下来要做的就是安排相亲了。因为过年时间并不是很长，所以姑姑希望能够尽可能在一天安排比较多的相亲。由于一个人同一天只能和一个人相亲，所以要从当前的相亲情况表里选择尽可能多的组合，且每个人不会出现两次。不知道有没有什么好办法，对于当前给定的相亲情况表，能够算出最多能同时安排多少组相亲呢？

同样的，我们先将给定的情况表转换成图G=(V,E)。在上一回中我们已经知道这个图可以被染成黑白两色。不妨将所有表示女性的节点记为点集A，表示男性的节点记为点集B。则有A∪B=V。由问题可知所有边e的两个端点分别属于AB两个集合。则可以表示成如下的图：

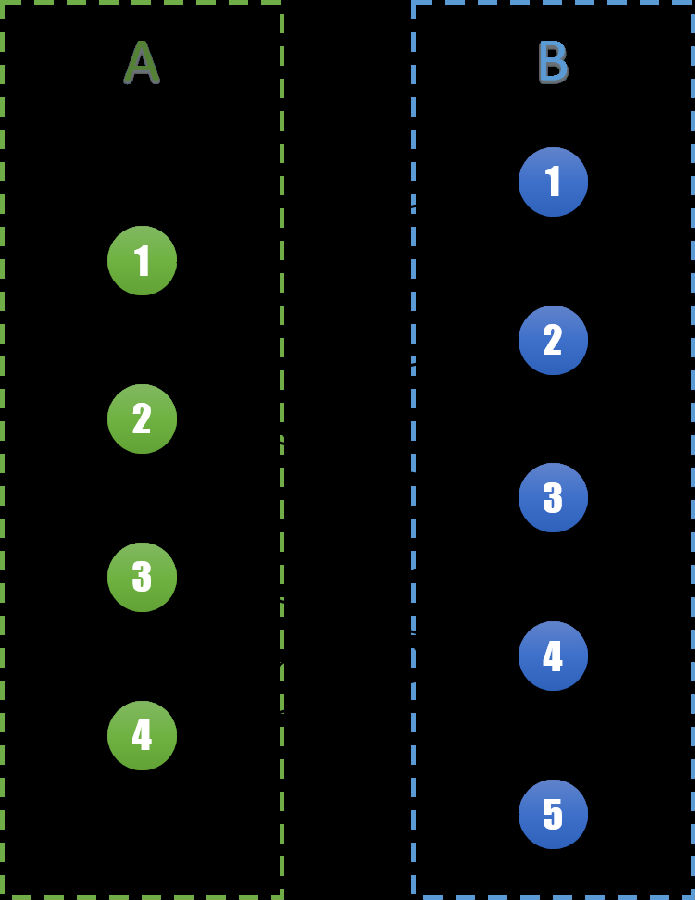
同样的，我们将所有的边分为两个集合。集合S和集合M，同样有S∪M=E。边集S表示在这一轮相亲会中将要进行的相亲，边集M表示在不在这一次进行。对于任意边(u,v) ∈ S，我们称u和v为一组匹配，它们之间相互匹配。在图G，我们将边集S用实线表示，边集M用虚线表示。得到下图：

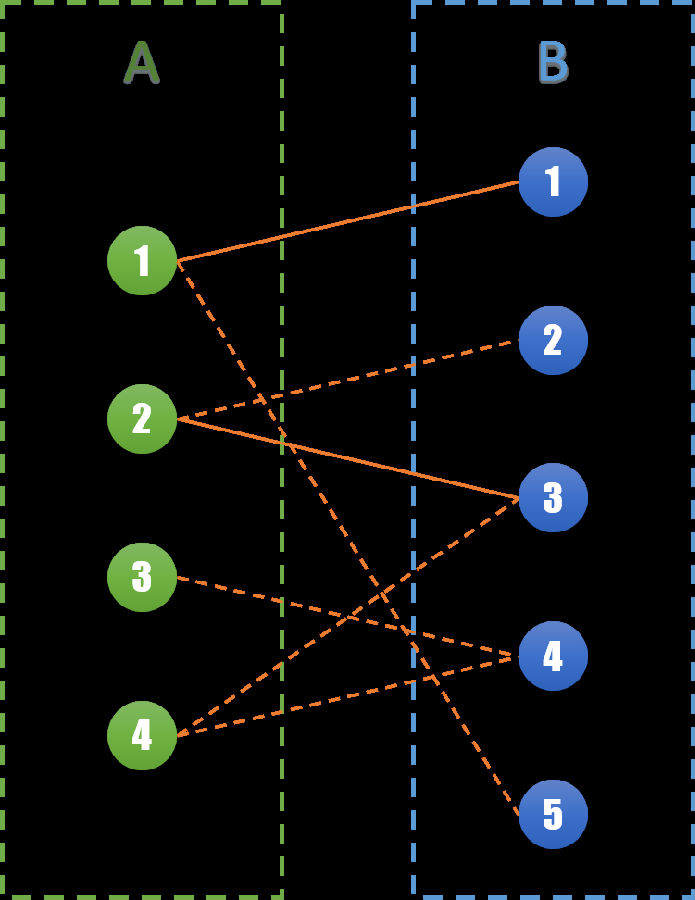
则原问题转化为，最多能选择多少条边到集合S，使得S集合中任何两条边不相邻(即有共同的顶点)。显然的，|S|<=Min{|A|, |B|}。

那么能不能找到一个算法，使得能够很容易计算出尽可能多的边能够放入集合S？我们不妨来看一个例子：

对于已经匹配的点我们先不考虑，我们从未匹配的点来做。这里我们选择A集合中尚未匹配的点(A3和A4)考虑：

对于A3点，我们可以发现A3与B4右边相连，且都未匹配。则直接将(A3,B4)边加入集合S即可。

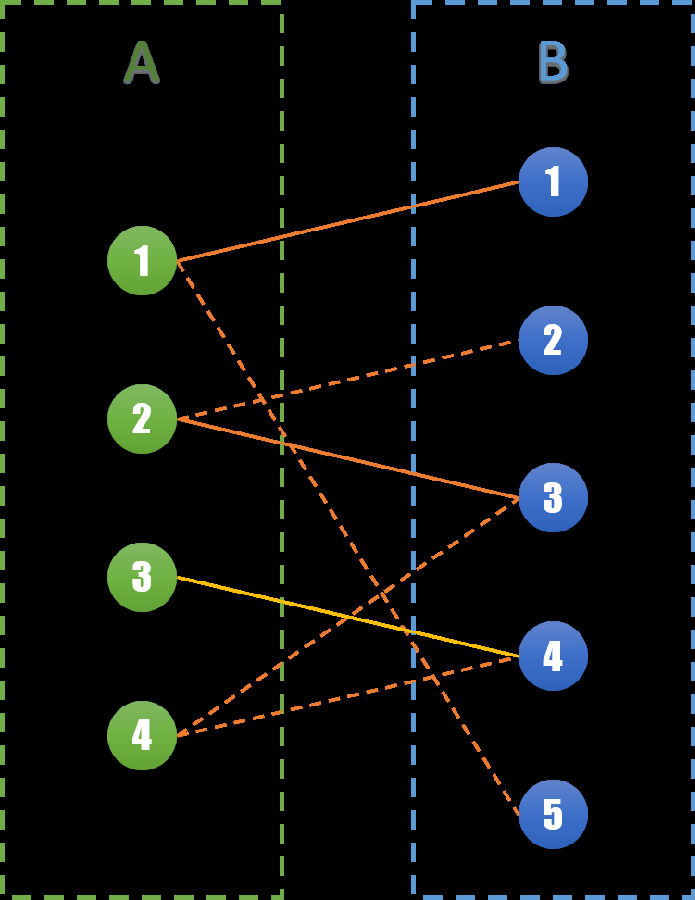
对于A4点，我们发现和A4相连的B3，B4点都已经匹配了。但是再观察可以发现，如果我们将A2和B2相连，则可以将B3点空出来。那么就可以同时将(A2,B2)，(A4,B3)相连。将原来的一个匹配变成了两个匹配。

让我们来仔细看看这一步：我们将这次变换中相关联的边标记出来，如下图所示紫色的3条边(A2,B2),(A2,B3),(A4,B3)。

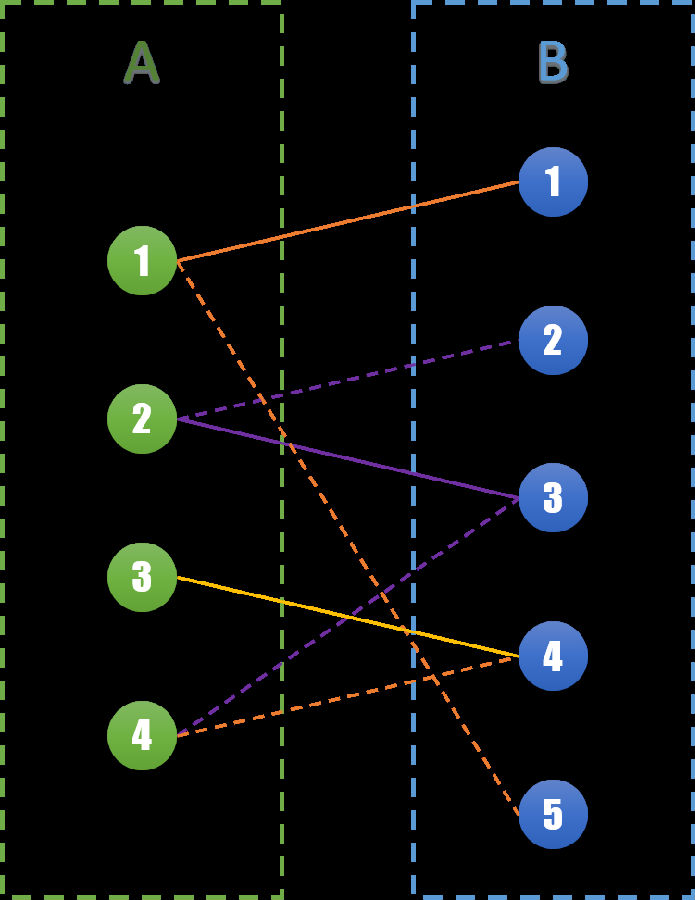
这三条边构成了一条路径，可以发现这条路径有个非常特殊的性质。虚线和实线相互交错，并且起点和终点都是尚未匹配的点，且属于两个不同的集合。我们称这样的路径为交错路径。

再进一步分析，对于任意一条交错路径，虚线的数量一定比实线的数量多1。我们将虚线和实线交换一下，就变成了下面的图：

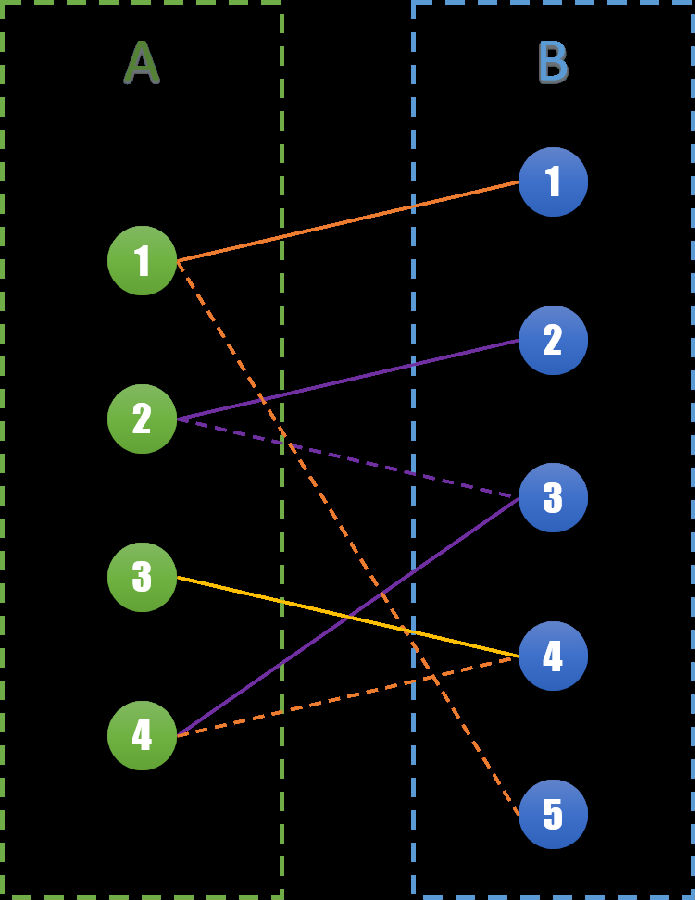
在原来1个匹配的基础上，我们得到了2个新的匹配，S集合边的数量也增加了1。并且原来在已经匹配的点仍然是已经匹配的状态。

再回头看看A3点匹配时的情况：对于(A3,B4)这一条路径，同样满足了交错路径的性质。

至此我们得到了一个找新匹配的有效算法：

选取一个未匹配的点，查找是否存在一条以它为起点的交错路径。若存在，将该交错路径的边虚实交换。否则在当前的情况下，该点找不到可以匹配的点。

又有对于已经匹配的点，该算法并不会改变一个点的匹配状态。所以当我们对所有未匹配的点都计算过后，仍然没有交错路径，则不可能找到更多的匹配。此时S集合中的边数即为最大边数，我们称为最大匹配数。

那么我们再一次梳理整个算法：

1. 依次枚举每一个点i； 
2. 若点i尚未匹配，则以此点为起点查询一次交错路径。

最后即可得到最大匹配数。

在这个基础上仍然有两个可以优化的地方：

1.对于点的枚举：当我们枚举了所有A中的点后，无需再枚举B中的点，就已经得到了最大匹配。
2.在查询交错路径的过程中，有可能出现Ai与Bj直接相连，其中Bj为已经匹配的点，且Bj之后找不到交错路径。之后又通过Ai查找到了一条交错路径{Ai,Bx,Ay,…,Az,Bj}延伸到Bj。由于之前已经计算过Bj没有交错路径，若此时再计算一次就有了额外的冗余。所以我们需要枚举每个Ai时记录B集合中的点是否已经查询过，起点不同时需要清空记录

输入

第1行：2个正整数，N,M(N表示点数 2≤N≤1,000，M表示边数1≤M≤5,000)
第2..M+1行：每行两个整数u,v，表示一条无向边(u,v)

输出

第1行：1个整数，表示最大匹配数

样例输入

5 4
3 2
1 3
5 4
1 5

样例输出

2

EmacsNormalVim

 

 

思考：如果是在无向图（并非树，不能树形DP做）中选择最多的边，使得这些边的顶点不相交。

不能染色，毕竟不一定满足check后不是男就是女。这样是否是NP问题。

 

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=;
const int maxm=;
int Laxt[maxm],Next[maxm],To[maxm],cnt;
int linke[maxn],vis[maxn],col[maxn],n;
void add(int u,int v)
{
    Next[++cnt]=Laxt[u];
    Laxt[u]=cnt;
    To[cnt]=v;
}
int read()
{
    char c=getchar();int s=;
    while(c>''||c<'') c=getchar();
    while(c>=''&&c<=''){s=s*+c-'';c=getchar();}
    return s;
}
bool find(int u)
{

    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(vis[v]||col[v]==) continue;
        vis[v]=;
        if(!linke[v]||find(linke[v])){
            linke[v]=u;
            return true;
        }
    }
    return false;
}
bool dfs(int v,int c)
{
    for(int i=Laxt[v];i;i=Next[i]){
        if(col[To[i]]==c) return false;
        if(!col[To[i]]){
            col[To[i]]=-c;
            if(!dfs(To[i],-c)) return false;
        }
    }
    return true;
}
bool check()
{
    for(int i=;i<=n;i++){
        if(col[i]) continue;
        col[i]=;
        if(!dfs(i,)) return false;
    }
    return true;
}
int main()
{
    int m,i,u,v,ans=;
    scanf("%d%d",&n,&m);
    for(i=;i<=m;i++) {
        u=read();v=read();
        add(u,v);
        add(v,u);
    }
    check();
    for(i=;i<=n;i++){
        if(col[i]==) {
           memset(vis,,sizeof(vis));
           if(find(i)) ans++;
        }
    }
    printf("%d\n",ans);
    return ;
}