连续因子一个正整数 N

一个正整数 N 的因子中可能存在若干连续的数字。例如 630 可以分解为 3×5×6×7，其中 5、6、7 就是 3 个连续的数字。给定任一正整数 N，要求编写程序求出最长连续因子的个数，并输出最小的连续因子序列。

输入格式：

输入在一行中给出一个正整数 N（1<N<2^31）。

输出格式：

首先在第 1 行输出最长连续因子的个数；然后在第 2 行中按 因子1*因子2*……*因子k 的格式输出最小的连续因子序列，其中因子按递增顺序输出，1 不算在内。

输入样例：

630

输出样例：

3
5*6*7

#include <iostream>
#include<cmath>
using namespace std;
int main()
{
    int length=0;
    int max_1=1;
    int  N;
    cin>>N;
    int N_2=sqrt(N);
    for(int i=2;i<=N_2;i++)
    {
        int length_1=0;
        int n=N;
        int x=i;
        while((n%x)==0)
        {
            n=n/x;
            length_1++;
            x++;
        }
        if(length_1>length)
        {
            length=length_1;
            max_1=--x;
        }
    }

    if(length>0)
    {
        cout<<length<<endl;
        for(int i=1;i<=length;i++)
    {
        cout<<max_1-length+i;
        if(i<length)cout<<"*";
    }
    }
    else
    {
        cout<<1<<endl;
        cout<<N;
    }
}

	一个正整数 N 的因子中可能存在若干连续的数字。例如 630 可以分解为 3×5×6×7，其中 5、6、7 就是 3 个连续的数字。给定任一正整数 N，要求编写程序求出最长连续因子的个数，并输出最小的连续因子序列。 输入格式： 输入在一行中给出一个正整数 N（1<N<2^31）。 输出格式： 首先在第 1 行输出最长连续因子的个数；然后在第 2 行中按 因子1*因子2*……*因子k 的格式输出最小的连续因子序列，其中因子按递增顺序输出，1 不算在内。 输入样例： 630 输出样例： 3 5*6*7 来自 <PTA | 程序设计类实验辅助教学平台>
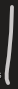			（1）先求能整除的所有因子数 （2）以（1）中的数为基础探求最大连续因子数

	#include <iostream> using namespace std; int main() { int N; cin>>N; int N_2; N_2=N/2; cout<<N_2<<endl; int i=0; for(i=2;i<N_2;i++) { // cout<<i; int xx; xx=N%i; if(xx==0) cout<<i<<"  "; } }

	#include <iostream> using namespace std; int main() { int q[9999]={0}; int N; cin>>N; int N_2; N_2=N/2; cout<<N_2<<endl; int i=0; int t=0; for(i=2;i<N_2;i++) { // cout<<i; int xx; xx=N%i; if(xx==0) {q[t]=i;t++} } for(i=0;i<t;i++) { int xx=0; for(;q[xx]<N_2;xx++) { if() } } }
		#include <iostream> #include<cmath> using namespace std; int main() { int length=0; int max_1; float N; cin>>N; int N_2=sqrt(N); for(int i=0;i<N_2;i++) { int length_1=0; int n=N; int x=i; while((n%i)!=0) { length_1++; n=n/x; x++; } if(length_1>length) { length=length_1; max_1=--x; } } cout<<length<<endl; for(int i=0;i<length;i++) { cout<<max_1-i; } }

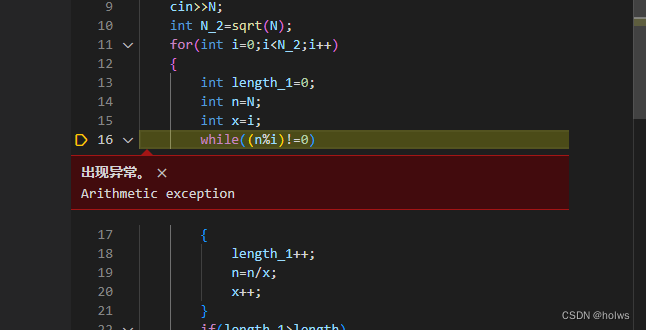输入样例：

630

输出样例：

3
5*6*7

cout<<--length<<endl;

for(int i=1;i<=length;i++)

{

cout<<max_1-length+i;

if(i<length)cout<<"*";

}

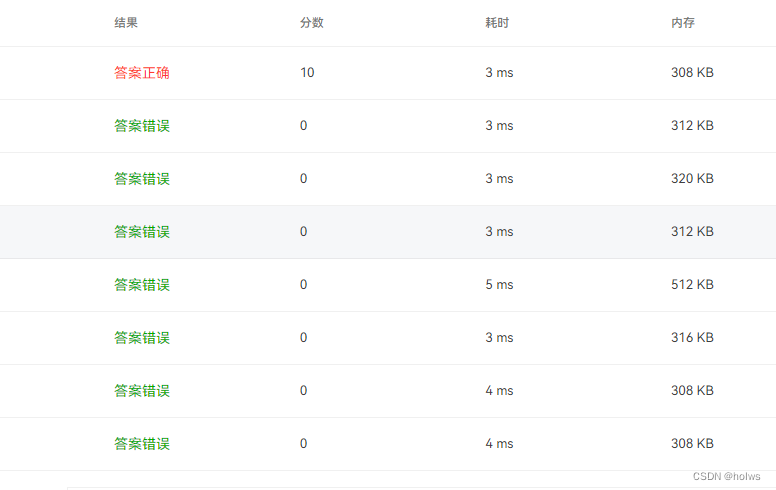
#include <iostream>

#include<cmath>

using namespace std;

int main()

{

int length=0;

int max_1=1;

int  N;

cin>>N;

int N_2=sqrt(N);

for(int i=2;i<=N_2;i++)

{

int length_1=0;

int n=N;

int x=i;

while((n%x)==0)

{

n=n/x;

length_1++;

x++;

}

if(length_1>length)

{

length=length_1;

max_1=--x;

}

}

if(length>0)

{

cout<<length<<endl;

for(int i=1;i<=length;i++)

{

cout<<max_1-length+i;

if(i<length)cout<<"*";

}

}

else

{

cout<<1<<endl;

cout<<N;

}

}

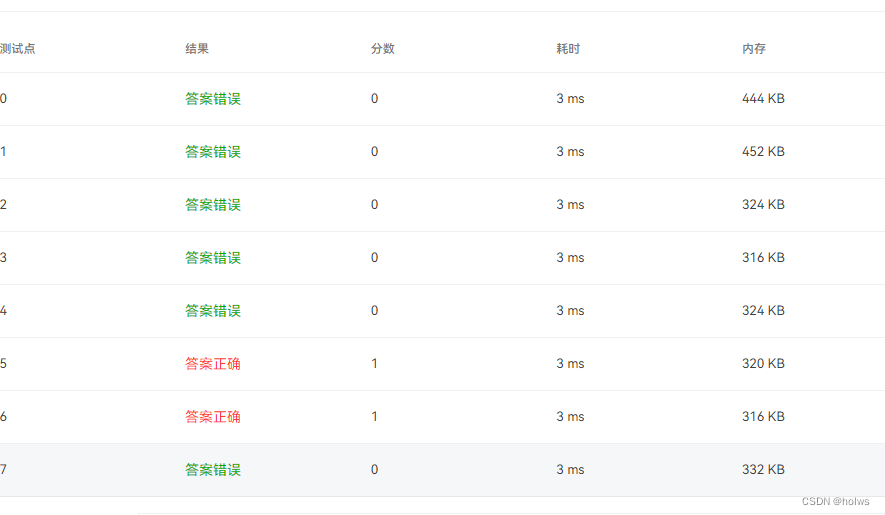			#include <iostream> int main() { int N; std::cin>>N; std::cout<<1<<std::endl<<N; }