重新整理数据结构与算法(c#)—— 二叉树排序树[二十二]

前言

什么是二叉堆排序呢?

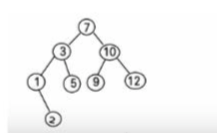
就是上面这种，一个节点大于左节点，但是小于右节点，再我写的例子中会写出大于等于右节点。

那么如何让一个数组进行变成这种二叉树呢？

其实只要有规律就很简单。

第一个元素（0）作为根节点。

第二个元素如果比第一个元素则判断是否有左节点，如果没有左节点，就是它的左节点，如果有左节点就和它的左节点比较。

正文

直接上代码吧:

public class BinarySortTree
{
	//根节点
	Node root;
	public BinarySortTree(Node root)
	{
		this.root = root;
	}

	public BinarySortTree() : this(null)
	{

	}

	public void add(Node node)
	{
		if (root == null)
		{
			root = node;
		}
		else
		{
			this.root.addNode(node);
		}
	}

	public void infixOrder()
	{
		if (root == null)
		{
			Console.WriteLine("root 为空");
		}
		else
		{
			root.infixOrder();
		}
	}

	public Node searchNode(int value)
	{
		if (root==null)
		{
			Console.WriteLine("root 为空");
		}
		return root.searchNode(value);
	}
}

public class Node
{
	public Node left;

	public Node right;

	int value;

	public int Value { get => value; set => this.value = value; }

	public Node(int value)
	{
		this.Value = value;
	}
	//中序排序
	public void infixOrder()
	{
		if (this.left != null)
		{
			this.left.infixOrder();
		}
		Console.WriteLine(this);
		if (this.right != null)
		{
			this.right.infixOrder();
		}
	}

	public override string ToString()
	{
		return Value.ToString();
	}
	//增加元素
	public void addNode(Node node)
	{
		if (node.Value < this.Value)
		{
			if (this.left == null)
			{
				this.left = node;
			}
			else
			{
				this.left.addNode(node);
			}
		}
		else {
			if (this.right == null)
			{
				this.right = node;
			}else {
				this.right.addNode(node);
			}
		}
	}
	//查找元素
	public Node searchNode(int value)
	{
		if (this.Value == value)
		{
			return this;
		}
		if (this.Value > value)
		{
			if (this.left != null)
			{
				return this.right.searchNode(value);
			}
			else
			{
				return null;
			}
		}
		else
		{
			if (this.left != null)
			{
				return this.left.searchNode(value);
			}
			else
			{
				return null;
			}
		}
	}
}

测试代码:

static void Main(string[] args)
{
	int[] arr = { 7, 3, 10, 12, 5, 1, 9, 2 };
	BinarySortTree binarySortTree = new BinarySortTree();
	//循环的添加结点到二叉排序树
	for (int i = 0; i < arr.Length; i++)
	{
		binarySortTree.add(new Node(arr[i]));
	}
	//中序遍历后的数据
	binarySortTree.infixOrder();
	Node node = binarySortTree.searchNode(7);
	Console.WriteLine("输入7，查找结果为:"+node.Value);
	//查找一个为空元素
	Node node100 = binarySortTree.searchNode(100);
	if (node100 == null)
	{
		Console.WriteLine("查找元素为空");
	}
	Console.Read();
}

测试结果:

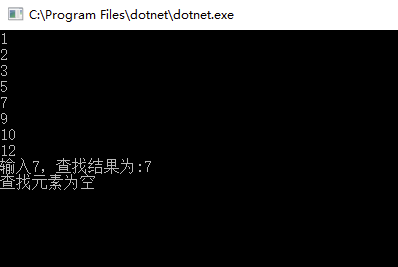
后面补一下删除节点的，看下以前的丢了不。