[转帖]find排除一个或多个目录的方法

find排除一个或多个目录的方法

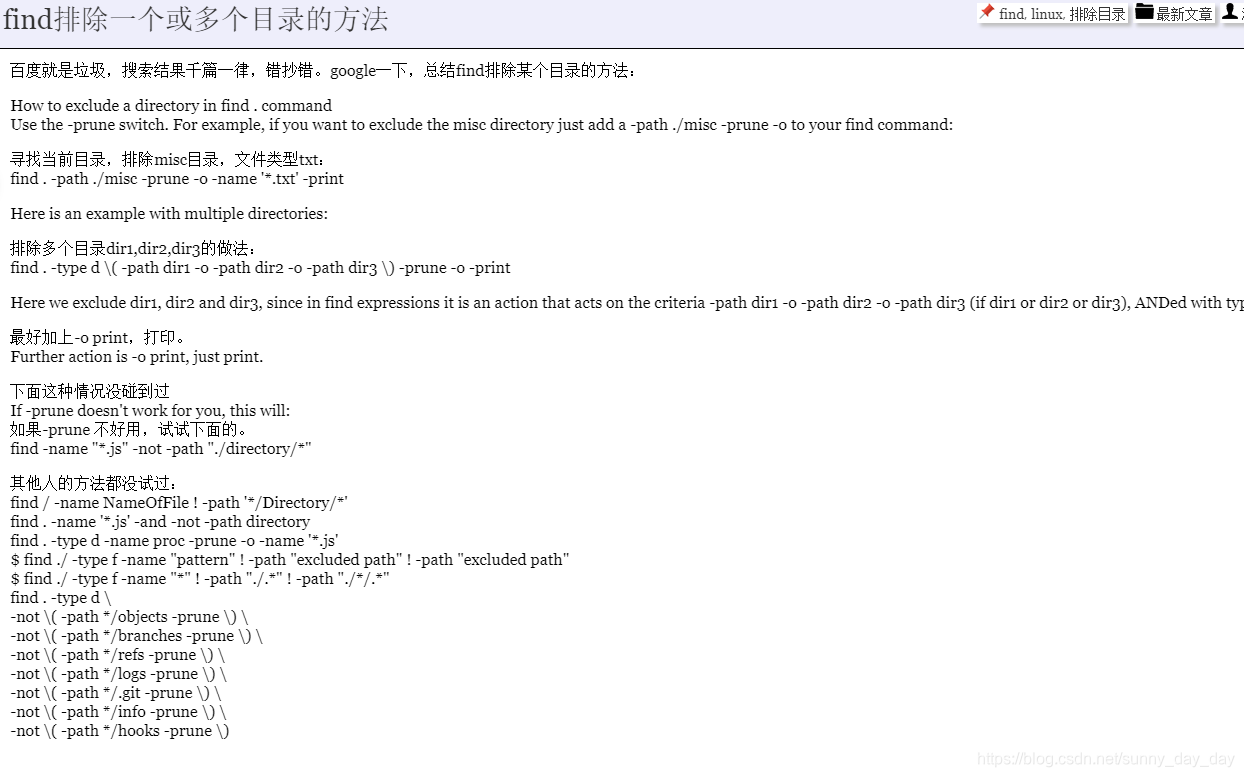
百度就是垃圾，搜索结果千篇一律，错抄错。google一下，总结find排除某个目录的方法：

How to exclude a directory in find . command
Use the -prune switch. For example, if you want to exclude the misc directory just add a -path ./misc -prune -o to your find command:

寻找当前目录，排除misc目录，文件类型txt：

find . -path ./misc -prune -o -name '*.txt' -print

Here is an example with multiple directories:

排除多个目录dir1,dir2,dir3的做法：

find . -type d \( -path dir1 -o -path dir2 -o -path dir3 \) -prune -o -print

Here we exclude dir1, dir2 and dir3, since in find expressions it is an action that acts on the criteria -path dir1 -o -path dir2 -o -path dir3 (if dir1 or dir2 or dir3), ANDed with type -d.

最好加上-o print，打印。

Further action is -o print, just print.

下面这种情况没碰到过

If -prune doesn’t work for you, this will:

如果-prune 不好用，试试下面的。

find -name "*.js" -not -path "./directory/*"

其他人的方法都没试过：

find / -name NameOfFile ! -path '*/Directory/*'
find . -name '*.js' -and -not -path directory
find . -type d -name proc -prune -o -name '*.js'
$ find ./ -type f -name "pattern" ! -path "excluded path" ! -path "excluded path"
$ find ./ -type f -name "*" ! -path "./.*" ! -path "./*/.*"
find . -type d \
-not \( -path */objects -prune \) \
-not \( -path */branches -prune \) \
-not \( -path */refs -prune \) \
-not \( -path */logs -prune \) \
-not \( -path */.git -prune \) \
-not \( -path */info -prune \) \
-not \( -path */hooks -prune \)