2022/07/16暑期集训考试 day1

T1 取餐号

看到数据范围 直接锁定埃氏筛和线性筛

我打的是一个优化一点的埃氏筛

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX = 5*1e6+50;
LL p[MAX],tot,n,m;
bool vis[MAX];
void work_p(LL n) {
	for(int i = 2; i <= n; i++) {
		if(vis[i] == 0) {
			p[++tot]=i;
		}
		for(int j = 1; j <= tot; j++) {
			if(p[j] * i > n) break;
			vis[p[j] * i] = 1;
		}
	}
}
int main() {
	freopen("number.in","r",stdin);
	freopen("number.out","w",stdout);
	scanf("%lld%lld",&n,&m);
	work_p(n);
	cout<<tot<<" "<<p[m];
	return 0;
}

时间复杂度 近似

O

（

n

l

o

g

n

）

O（n log n）

O（nlogn）
得分 100

T2 堆人塔

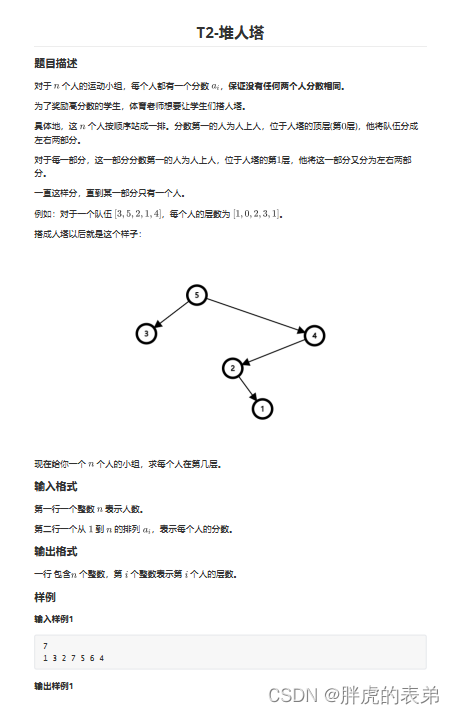
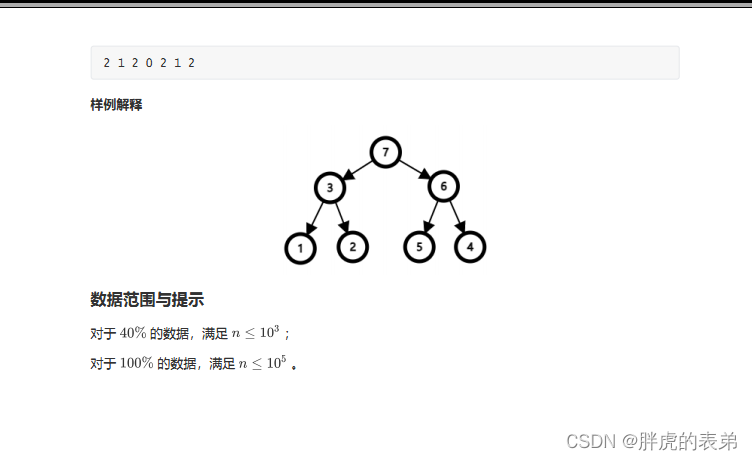
思路 : 首先根据题意 得到 过程 ，找到当前区间最大的一个值，将这个值编号，分成左右两个区间，在进行查找最大值。可以dfs查找区间，for循环枚举找到最大值，显然会被卡，可以通过ST表进行预处理，

O

(

1

)

O(1)

O(1) 得出最大值。考场忘记了ST表的板子 打了40分的暴力
AC代码

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX = 1e5+30;
int n,a[MAX],ans[MAX],mx[110000][20];
bool bol1 = 1,bol2 = 1;//1—n，n-1;
bool vis[MAX];
void ST(){
    for(int i=1;i<=n;i++)
    	mx[i][0]=i;
    for(int j=1;(1<<j)<=n;j++)
        for(int i=1;i+(1<<j)<=n+1;i++){
        	if(a[mx[i][j - 1]] > a[ mx[i + (1 << (j - 1))] [j-1]])
        		mx[i][j] = mx[i][j - 1];
        	else
        		mx[i][j] = mx[i + ( 1 << (j - 1) )][j - 1];
		}
}
void dfs(int l, int r, int c) {
//	cout<<"*";
	if(l < 1|| r > n) return ;
	if(l > r) return ;
	if(l == r) {
		ans[l] = c;
		return ;
	}
  	int k=log2(r-l+1),ww;
  	int x = mx[l][k];
	int y = mx[r - (1 << k) + 1][k];
	if(a[x] > a[y]) ww = x;
	else ww = y;
	ans[ww] =c;
	dfs(ww + 1, r, c+1);
	dfs(l, ww-1, c+1);
}
int main() {
	freopen("tower.in","r",stdin);
	freopen("tower.out","w",stdout);
	scanf("%d",&n);
	for(int i = 1; i <= n ;i++)
			scanf("%d",&a[i]);
	ST();
	dfs(1,n,0);// nlogn -> n!
	for(int i = 1; i <= n; i++) {
		if(i == 1) printf("%d",ans[i]);
		else printf(" %d",ans[i]);
	}
	return 0;
}

T3

思路 :没有思路 暴力（还是一个错误的假暴力（哭））

正解

{

二分 中位数

O（n） 的将 大于 中位数 的 数 值 附上1

将 小于 中位数 的数值 附上-1

算出前缀和

如果存在一个区间满足 区间和 >= 0，则必定存在大于等于 当前mid 的值

返回 1；

否则返回 0

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX = 1e5+60;
LL n, k, a[MAX], res = 0,sum[MAX];
bool check(LL mid) {
	for(int i = 1; i <= n; i++) {
		sum[i] = sum[i-1];
		if(a[i] >= mid) sum[i]++;
		else sum[i]--;
	}
	LL minn = 1e9;
	for(int i = k+1; i <= n; i++) {
		if(sum[i - k] < minn) minn = sum[i - k];
		if(sum[i] - minn > 0) return 1;
	}
	return 0;
}
int main() {
	freopen("plunder.in","r",stdin);
	freopen("plunder.out","w",stdout);
	scanf("%lld%lld", &n, &k);
	for(int i = 1 ;i <= n; i++)
		scanf("%lld",&a[i]);
	LL l = 1, r = 1e9+1;
	while(l + 1 < r) {
		LL mid = (l + r) >> 1 ;
		if(check(mid)) {
			res = mid;
			l = mid;
		}
		else r = mid;
	}
	cout<<res;
	return 0;
}

}

T4 攻打恶魔之巅

思路 : dp,

f

[

i

]

[

j

]

f[i][j]

f[i][j]表示在第i个台阶还剩j个能量石的最小步数

f

[

i

+

k

]

[

j

]

=

m

i

n

(

f

[

i

+

k

]

[

j

]

,

f

[

i

]

[

j

]

+

1

)

f[i + k][j] = min(f[i+k][j] , f[i][j] +1 )

f[i+k][j]=min(f[i+k][j],f[i][j]+1)
如果有传送阵得到

f

[

t

[

i

]

]

[

j

−

1

]

=

m

i

n

(

f

[

t

[

i

]

]

[

j

−

1

]

,

f

[

i

]

[

j

]

)

f[t[i]][j-1]=min(f[t[i]][j-1],f[i][j])

f[t[i]][j−1]=min(f[t[i]][j−1],f[i][j])

正解：
但这个方程显然有后效性，即使用传送阵 后边的最小值可以修改前边的最小值
为了避免后效性 我们以 能量石作为状态 ，枚举往前走k距离，在枚举往后走k距离

#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MAX = 5*1e6+50,oo=1e9;
LL f[MAX][30],n,m,k,t[MAX],ans=1e9;//表示 在第i个楼梯 还剩 k 能量石 最小步数
int main()
{
	freopen("step.in","r",stdin);
	freopen("step.out","w",stdout);
	scanf("%lld%lld%lld",&n,&m,&k);
	for(int i = 1; i <= n ;i++)
		scanf("%lld",&t[i]);
	for(int i = 0; i <= n; i++)
		for(int j = 0; j <= k; j++)
			f[i][j] = oo;
	f[1][k] = 0;
	for(int j = k; j>= 0; j--) {
		for(int i = 1; i <= n; i++) {
			for(int mm = 1; mm <= m; mm++) {
				if(mm + i > n) break;
				f[mm+i][j]=min(f[mm+i][j],f[i][j] + 1);
			}
			if(j>=1)
			f[t[i]][j-1] =min(f[t[i]][j-1],f[i][j]);
		}
		for(int i = n; i >= 1 ;i-- ){
			for(int mm = 1; mm <= m; mm++) {
				if(i <= mm) break;
				f[i-mm][j] = min(f[i-mm][j],f[i][j] + 1);
			}
			if(j>=1)
			f[t[i]][j-1] =min(f[t[i]][j-1],f[i][j]);
		}
	}

	for(int i = 0; i <= k ;i++)  ans = min(ans,f[n][i]);
	cout<<ans<<endl;
	return 0;
}

T5

不会

得分 : 100+40+20+0+15=175
*