解决Few-shot问题的两大方法：元学习与微调

.center { width: auto; display: table; margin-left: auto; margin-right: auto }

基于元学习（Meta-Learning）的方法：

Few-shot问题或称为Few-shot学习是希望能通过少量的标注数据实现对图像的分类，是元学习(Meta-Learning)的一种。

Few-shot学习，不是为了学习、识别训练集上的数据，泛化到测试集，而是为了让模型学会学习。也就是模型训练后，能理解事物的异同、区分不同的事物。如果给出两张图片，不是为了识别两张图片是什么，而是让模型知道两张图片是相同的事物还是不同的事物。

Few-shot可以被定义为K-way，N-shot问题，表示支持集有k个类别，每个类别有n个样本。不同于训练深度深度神经网络每个类有大量样本的数据集，Few-shot的训练数据集规模很小

Meta-Learning的核心思想就是先学习到一个先验知识（prior），这需要经历多个task的训练，每个task的分为支持集（support set）和查询集（query set），支持集包含了k个类、每个类n张图，模型需要对查询集的样本进行归类以训练模型的学习能力。

经过了很多个task学习先验知识，才能解决新的task，新的task涉及的类，不包含在学习过的task！ 我们把学习训练的task称为meta-training task，新的task称为meta-testing task。最后的评价指标就是根据红色部分表现结果。

meta training task
support	query
support	query
...
support	query

meta testing task
support	query

需要注意查询集和测试集的区别，因为在Few-shot训练过程也有查询集，在Few-shot测试中，接触的支持集和测试集都是全新的类。

Supervised Learning vs. Few-shot Learning

传统监督学习	Few-shot 学习
测试样本未在训练集中见过	查询样本没见过
测试样本的类在训练集中见过	查询样本的类属于未知

基于微调（Fine-Tuning）的方法：

基于微调的Few-shot方法封为三个步骤：

1. 预训练：使用模型在大规模的数据集进行预训练作为特征提取器\(f\)。
2. 微调：在支持集上训练分类器。
3. Few-shot预测：
   1. 将支持集上的图像通过分类器转为特征向量；
   2. 对每一个类的特征向量求平均，得到类的特征向量：\(\mu_1,\dots,\mu_k\)；
   3. 将查询的特征与\(\mu_1,\dots,\mu_k\)比较。

先省略第二步的微调，看看一般的预训练Few-shot预测。

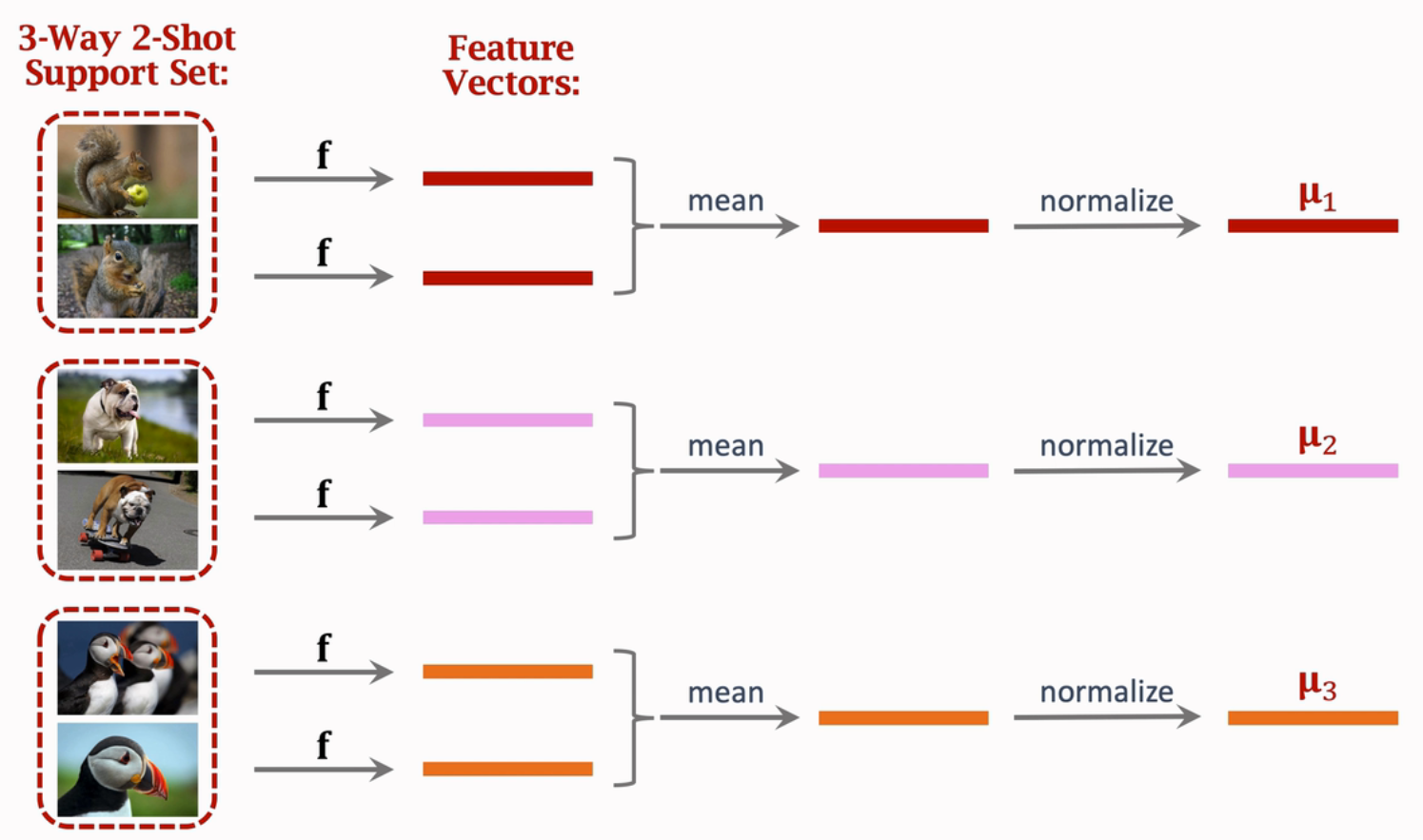
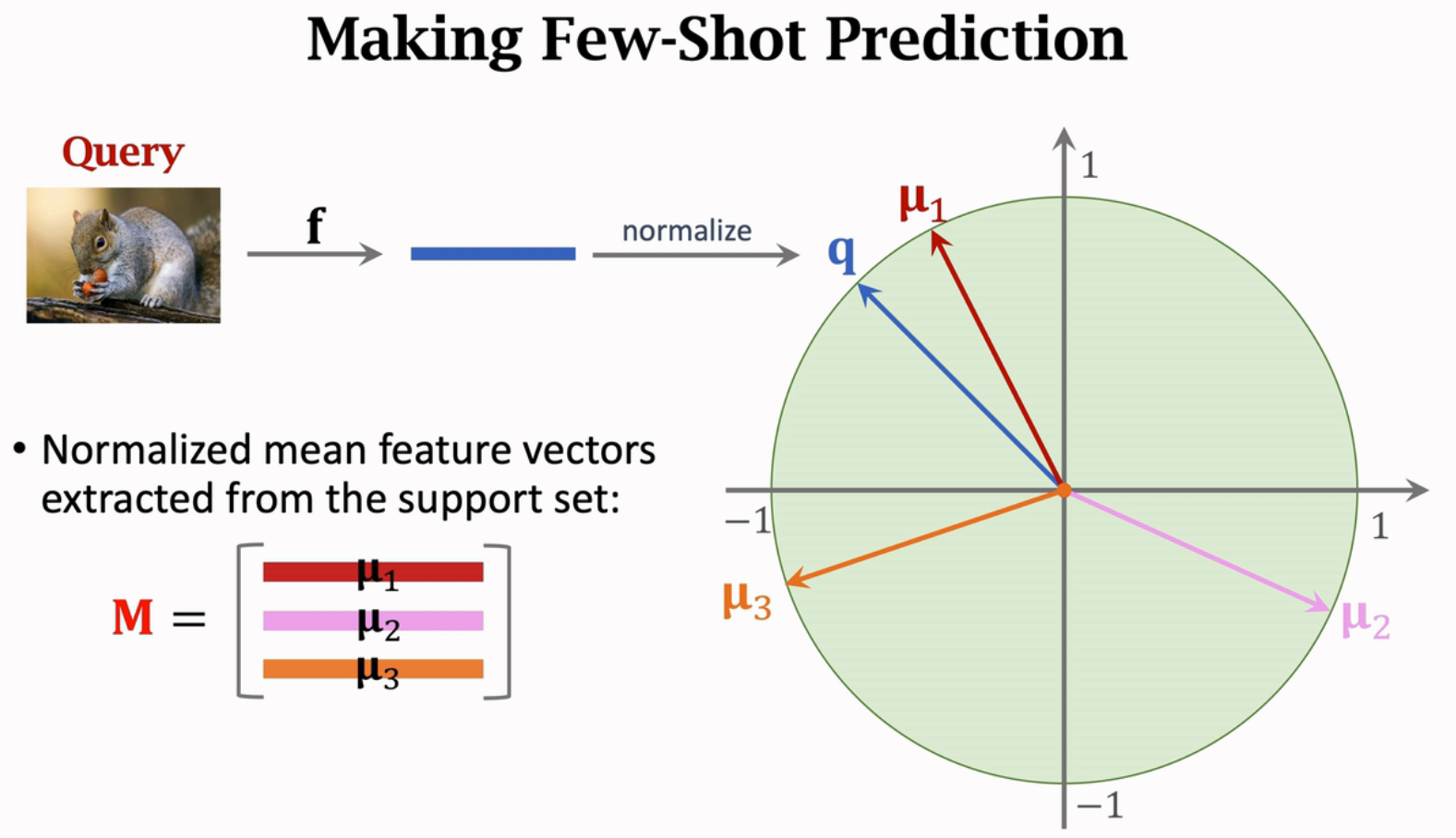
以上图为例，将每一个类的平均特征堆叠得到矩阵\(M\in\mathbb{R}^{3\times n}\)，这里\(n\)表示特征数。

\[M =\begin{bmatrix} \mu_1 \\ \mu_2 \\ \mu_3 \end{bmatrix}\tag{1}
\]

将查询的图片提取特征、做归一化得到\(q\in\mathbb{R}^{1\times n}\)，并进行预测。

\[p = \mathrm{Softmax}(Mq) \tag{2} = \mathrm{Softmax}(\begin{bmatrix} \mu_1^Tq \\ \mu_2^Tq \\ \mu_3^Tq \end{bmatrix})
\]

本例中，输出的第一类的概率最大。

归纳一下上述使用预训练模型预测查询集图像的步骤：

1. 设置查询集的标记样本：\((x_j,y_j)\)。
2. 用预训练模型提取特征：\(f(x_j)\)。
3. 进行预测：\(p_j = \mathrm{Softmax}(W\cdot f(x_j)+b)\)。

以上固定了\(W=M, b=2\)。但可以在支持集进行训练，微调\(W\)和\(b\)。于是设置损失函数去学习\(W\)和\(b\)，由于支持集较小，需要加入正则项防止过拟合：

\[\min\sum_j\mathrm{CrossEntropy}(y_j,p_j)+\mathrm{Regularization}\tag{3}
\]

大量实验证明，微调确实能提高精度。以下是一些常用的技巧：

1. 对于预测分类器\(p=\mathrm{Softmax}=(W\cdot f(x)+b)\)，可以进行初始化\(W=M,b=0\)。
2. 对于正则项的选择可以考虑Entropy Regularization，相关的解释可以参考文献[3]。
3. 将余弦相似度加入Softmax分类器，即：

\[p=\mathrm{Softmax}=(W\cdot f(x)+b)=\mathrm{Softmax}(\begin{bmatrix}
w^T_1q+b_1 \\
w^T_2q+b_2 \\
w^T_3q+b_3
\end{bmatrix})
\\ \Downarrow
\\
p=\mathrm{Softmax}(\begin{bmatrix}
\mathrm{sim}(w_1,q)+b_1 \\
\mathrm{sim}(w_2,q)+b_2 \\
\mathrm{sim}(w_3,q)+b_3
\end{bmatrix}) \tag{4}
\]

其中\(\mathrm{sim}=\frac{w^Tq}{\lVert w\rVert_2\cdot \lVert q\rVert_2}\)。

对比

基于两种方式解决Few-shot问题的对比

	元学习（Meta-Learning）	微调（Fine-Tuning）
策略	基于元学习的方法旨在通过在元任务上训练来使模型学会更好地适应新任务。它们通常涉及在多个元任务（task）上进行训练，以使模型能够从不同任务中学到共性。	基于微调的方法通常涉及在一个预训练的模型上进行微调，以适应特定的 few-shot 任务。在训练阶段，模型通常会使用大规模的数据集进行预训练，然后在少量训练数据上进行微调。
适用性	基于元学习的方法特别适用于 few-shot 任务，因为它们的目标是使模型从少量示例中快速学习。它们在少量数据和新任务上通常表现出色。	基于微调的方法在具有大量预训练数据的情况下通常表现出色。它们适用于很多不同类型的任务，但在数据稀缺或新领域的 few-shot 问题上可能表现不佳。
泛化能力	基于元学习的方法旨在提高模型在新任务上的泛化能力，因为它们通过从多个元任务中学习共性来实现这一目标。它们在适应新任务和未见数据上的表现通常较好。	基于微调的方法通常在预训练领域上有较强的泛化能力，但在新任务上的泛化能力可能有限，特别是当训练数据非常有限时。

参考文献

1. Few-shot learning（少样本学习）入门
2. Few-shot learning（少样本学习）和 Meta-learning（元学习）概述
3. 小样本学习 Few-Shot Learning