2D空间中比较两三角形相交与包含

在处理UV重叠、CPU的ZFighting检测时会遇到2D空间中的三角形相交问题，

网上普遍是3D空间的相交解法，因此写本文研究下，不过虽然实现了需求，

但用的方法比较暴力。

效果如图：

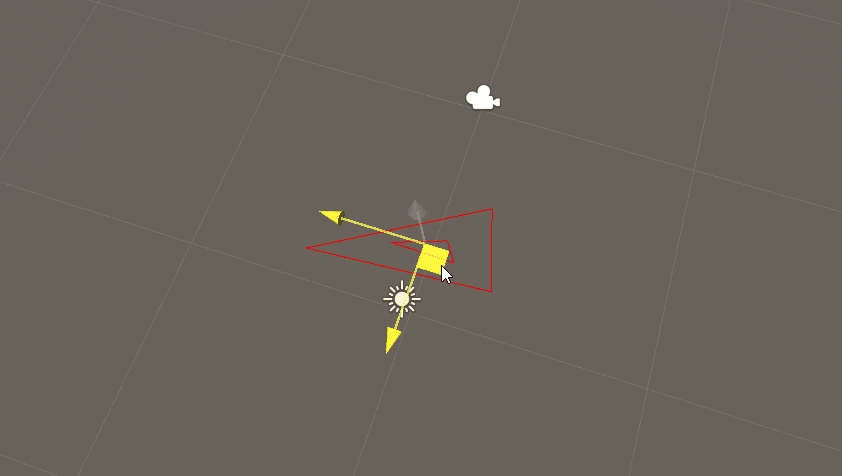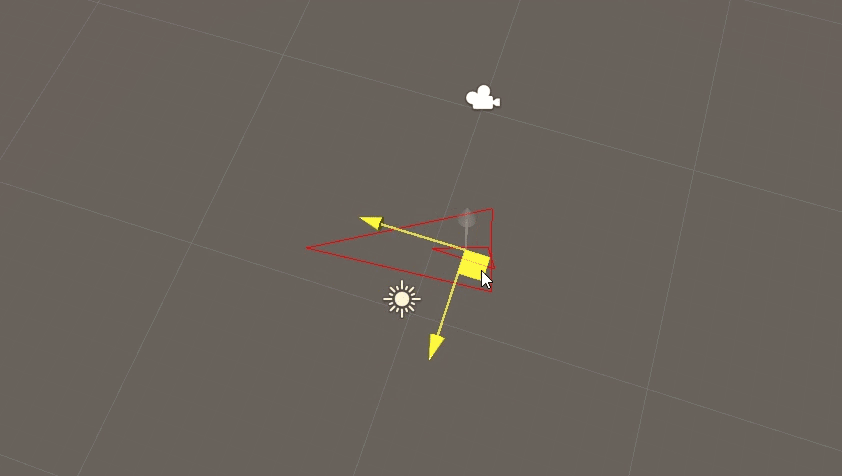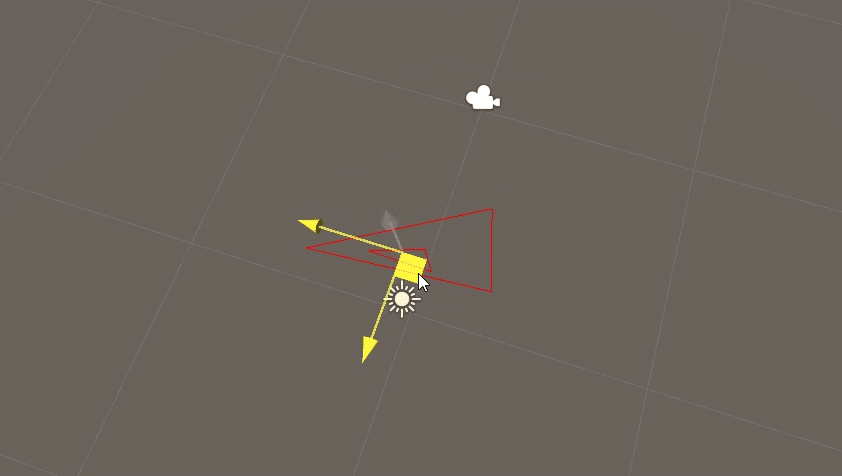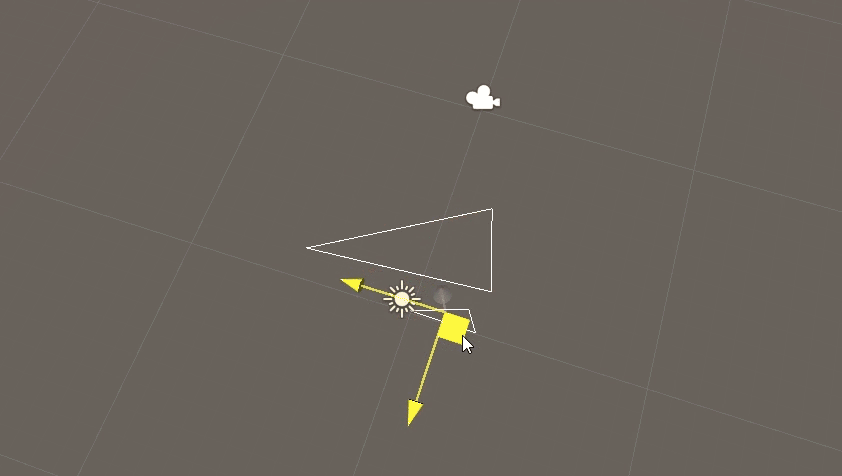
（鼠标拖动区域处有一小三角形，与外部大三角形进行相交包含演示）

若两三角形存在线段相交，则两三角形相交，但三点都包含的情况下则无法囊括在内。

所以还需额外判断一次三点都包含的情况。

2D空间的三角形相交得从线段与线段相交做起，这里用之前的叉乘方法来检测：

https://www.cnblogs.com/hont/p/6106043.html

点是否在多边形内用的是单双数检测法：

https://www.cnblogs.com/hont/p/6105997.html

方法还是比较朴素的方法，但离线情况下使用无问题。

代码如下(Unity XZ空间)：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class RayVsTriangle : MonoBehaviour
{
    public Transform a0;
    public Transform b0;
    public Transform c0;

    public Transform a1;
    public Transform b1;
    public Transform c1;

    private bool TriangleVsTriangle(Vector3 a0, Vector3 b0, Vector3 c0, Vector3 a1, Vector3 b1, Vector3 c1)
    {
        bool IsIntersect(Vector3 a, Vector3 b, Vector3 c, Vector3 d)
        {
            float crossA = Vector3.Cross(d - c, a - c).y;
            float crossB = Vector3.Cross(d - c, b - c).y;

            if (!(crossA > 0f ^ crossB > 0f)) return false;

            float crossC = Vector3.Cross(b - a, c - a).y;
            float crossD = Vector3.Cross(b - a, d - a).y;

            if (!(crossC > 0f ^ crossD > 0f)) return false;

            return true;
        }

        bool IsContain(Vector3 a, Vector3 b, Vector3 c, Vector3 p0)
        {
            const float kRaycastLen = 100000f;

            Vector3 comparePoint = (c + b) * 0.5f;
            Vector3 originPoint = p0;
            comparePoint += (comparePoint - originPoint).normalized * kRaycastLen;

            int count = 0;
            if (IsIntersect(a, b, originPoint, comparePoint)) ++count;
            if (IsIntersect(b, c, originPoint, comparePoint)) ++count;
            if (IsIntersect(c, a, originPoint, comparePoint)) ++count;

            return count % 2 == 1;
        }

        if (IsIntersect(a0, b0, a1, b1)) return true;
        if (IsIntersect(a0, b0, b1, c1)) return true;
        if (IsIntersect(a0, b0, c1, a1)) return true;

        if (IsIntersect(b0, c0, a1, b1)) return true;
        if (IsIntersect(b0, c0, b1, c1)) return true;
        if (IsIntersect(b0, c0, c1, a1)) return true;

        if (IsIntersect(c0, a0, a1, b1)) return true;
        if (IsIntersect(c0, a0, b1, c1)) return true;
        if (IsIntersect(c0, a0, c1, a1)) return true;

        if (IsContain(a1, b1, c1, a0) && IsContain(a1, b1, c1, b0) && IsContain(a1, b1, c1, c0))
            return true;

        return false;
    }

    private void OnDrawGizmos()
    {
        bool isRed = TriangleVsTriangle(a0.position, b0.position, c0.position, a1.position, b1.position, c1.position);

        Gizmos.color = isRed ? Color.red : Color.white;

        Gizmos.DrawLine(a0.position, b0.position);
        Gizmos.DrawLine(b0.position, c0.position);
        Gizmos.DrawLine(c0.position, a0.position);

        Gizmos.DrawLine(a1.position, b1.position);
        Gizmos.DrawLine(b1.position, c1.position);
        Gizmos.DrawLine(c1.position, a1.position);
    }
}