【LeetCode剑指offer 02】矩阵中的路径（老鼠走迷宫plus，应用深度优先搜索与回溯机制）

矩阵中的路径

https://leetcode.cn/problems/ju-zhen-zhong-de-lu-jing-lcof/

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 "ABCCED"（单词中的字母已标出）。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"

输出：true

示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"

输出：false

提示：

m == board.length

n = board[i].length

1 <= m, n <= 6

1 <= word.length <= 15

board 和 word 仅由大小写英文字母组成

思路

这题其实就是经典的算法题“老鼠走迷宫”的变体，在老鼠走迷宫中，我们要避开障碍，找到通往出口的路径

这里也一样，只不过"障碍"变成了非目标字符，"通往出口的路径"就是我们的目标字符串

参考走迷宫的解法，我们要逐层遍历矩阵（迷宫），同时判断当前遍历值的下一步遍历位置是否满足要求，不满足要求就要换方向走，直到找到满足要求的方向再继续遍历（前进）

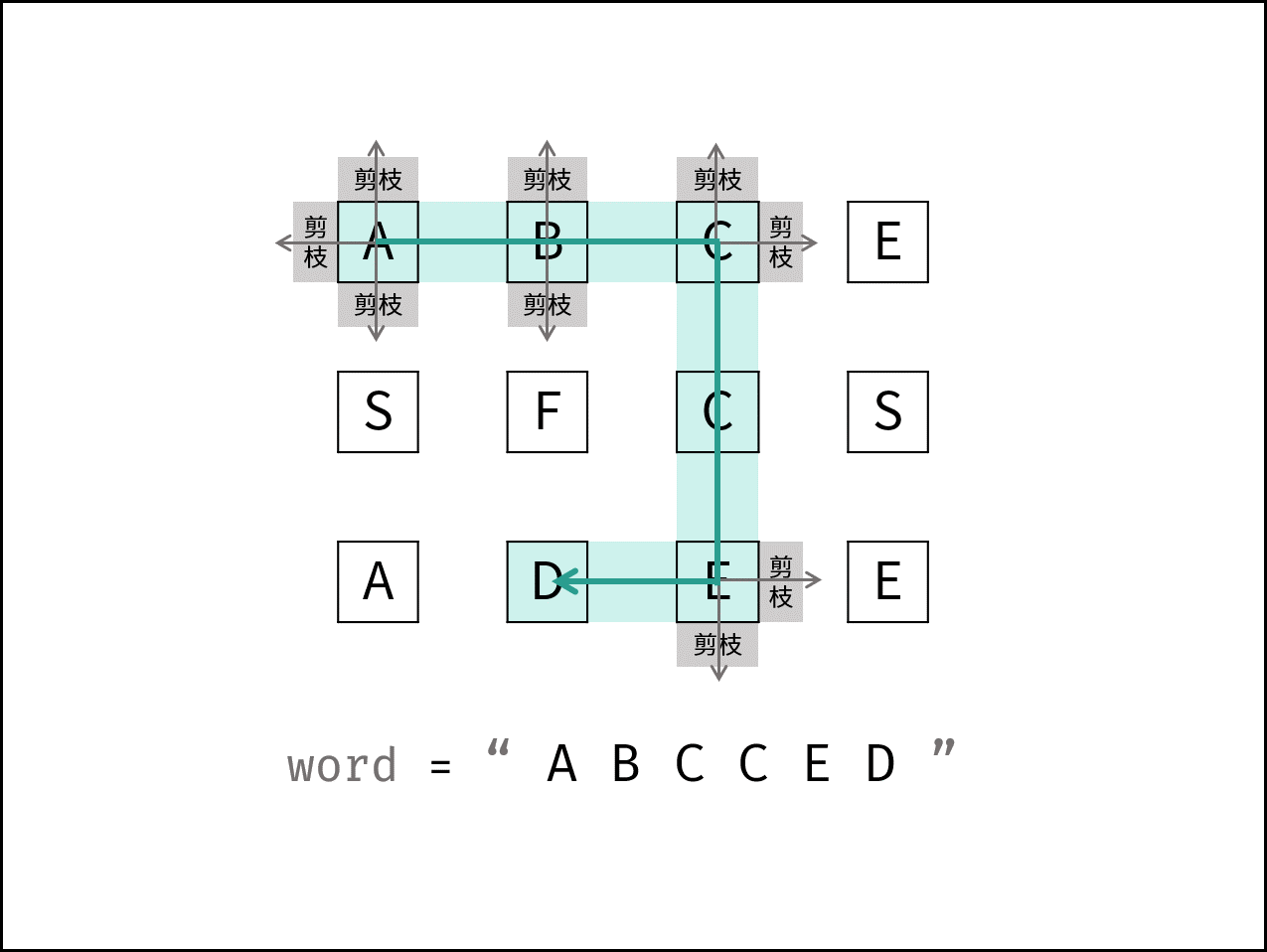
借一下k神的图，上面描述的过程即如图中所示

一般来说，知道老鼠走迷宫的，想出本题的解题思路应该不难，但是代码实现就有点难写

代码

实现上，根据分析，肯定是需要使用回溯机制的，也就是要用递归去实现（本题就是经典的深度优先搜索题）

老规矩，按照三部曲去分析一下

代码分析

1、确定递归函数参数与返回值

因为需要对不同前进方向的状态进行确认，因此递归函数需要返回值，且类型为布尔类型

需要的参数有：待搜索的矩阵board、目标字符串word、前进方向i、j,以及当前目标字符在word中的索引k

注意点：

1、前进方向i、j是需要一个约束边界的，因此还需定义两个变量来保存矩阵的行列大小

2、这里我们需要引入一个变量k来标记当前遍历值（如果是目标字符串中的字符）位于目标字符串中的下标，这样才可以避免出现重复使用某个值的情况

class Solution {
private:
    //定义变量保存数组的行列
    int rows, cols;
    //确定递归函数的参数与返回值
    bool dfs(vector<vector<char>>& board, string word, int i, int j, int k){

    }
public:
    bool exist(vector<vector<char>>& board, string word) {

    }
};

2、确定终止条件

终止条件有两类：非法情况和搜索完成情况

非法情况

即遍历过程中出现的各种非法情况，以及当前遍历值不是目标字符的情况

例如当前遍历值不是要检查上下左右四个方向哪边能继续走嘛，万一某个方向超出矩阵大小范围，这就属于一类触发递归终止的条件

如果遍历值都没出现在目标字符串word中，就直接不用往该方向走了

搜索完成

k用于指示当前找到了目标字符串中的哪个字符，如果k指向word的最后一个字符，那么意味着搜索结束，返回true

class Solution {
private:
    //定义变量保存数组的行列
    int rows, cols;
    //确定递归函数的参数与返回值
    bool dfs(vector<vector<char>>& board, string word, int i, int j, int k){
         //首先确定返回false的情况
        //i(行)、j(列)越界、当前矩阵遍历值不是目标字符串中的字符
        if(i >= rows || i < 0 || j >= cols || j < 0 || board[i][j] != word[k]) return false;
        //然后确定返回true的情况
        //k用于记录当前为目标字符的遍历值在目标字符串中的位置，当k以及在目标字符串末尾，就说明所有字符均已找到
        if(k == word.size() - 1) return true;
    }
public:
    bool exist(vector<vector<char>>& board, string word) {

    }
};

3、处理单层逻辑

在当前递归层中，我们需要先将当前遍历值填充为'0'（其实就是初始化一下矩阵，因为还不知道这个新的位置是否满足条件）

然后调用递归函数dfs去当前遍历值的四个方向（上下左右）去判断哪个方向可以走下一步，直到找到可以走的方向，并把当前遍历值位置的值改为对应目标字符串中k位置的字符，然后重复上述流程，判断下一个遍历位置是否满足条件

class Solution {
private:
    //定义变量保存数组的行列
    int rows, cols;
    //确定递归函数的参数与返回值
    //递归函数中，需要对不同前进方向的状态进行确认，因此返回值是布尔类型
    //需要的参数有：待搜索的矩阵board、目标字符串word、前进方向i、j,以及当前目标字符在word中的索引k
    bool dfs(vector<vector<char>>& board, string word, int i, int j, int k){
        //首先确定返回false的情况
        //i(行)、j(列)越界、当前矩阵遍历值不是目标字符串中的字符
        if(i >= rows || i < 0 || j >= cols || j < 0 || board[i][j] != word[k]) return false;
        //然后确定返回true的情况
        //k用于记录当前为目标字符的遍历值在目标字符串中的位置，当k以及在目标字符串末尾，就说明所有字符均已找到
        if(k == word.size() - 1) return true;

        //先当前遍历值统一填充为0（因为还不知道这个新的位置是否满足条件）
        board[i][j] = '0';
        //递归调用dfs对当前遍历值的下一个位置进行判断（上下左右）
        bool res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1)
                    || dfs(board, word, i, j - 1, k + 1) || dfs(board, word, i, j + 1, k + 1);
        //如果四个方向中有一个走得通（即返回true），那就把矩阵中当前位置的字符修改为目标字符串中k指向的相应字符
        //该操作是在最深的一层递归中完成的
        board[i][j] = word[k];

        return res;//向上一层递归返回本层递归结果

    }
public:
    bool exist(vector<vector<char>>& board, string word) {

    }
};

完整代码

主函数中，需要获取矩阵的行列（别搞混）

然后使用两层for循环遍历矩阵，调用递归判断结果，如果递归函数返回的是true，那么就结束

如果for遍历结束都没返回，那就返回false

class Solution {
private:
    //定义变量保存数组的行列
    int rows, cols;
    //确定递归函数的参数与返回值
    //递归函数中，需要对不同前进方向的状态进行确认，因此返回值是布尔类型
    //需要的参数有：待搜索的矩阵board、目标字符串word、前进方向i、j,以及当前目标字符在word中的索引k
    bool dfs(vector<vector<char>>& board, string word, int i, int j, int k){
        //首先确定返回false的情况
        //i(行)、j(列)越界、当前矩阵遍历值不是目标字符串中的字符
        if(i >= rows || i < 0 || j >= cols || j < 0 || board[i][j] != word[k]) return false;
        //然后确定返回true的情况
        //k用于记录当前为目标字符的遍历值在目标字符串中的位置，当k以及在目标字符串末尾，就说明所有字符均已找到
        if(k == word.size() - 1) return true;

        //先当前遍历值统一填充为0（因为还不知道这个新的位置是否满足条件）
        board[i][j] = '0';
        //递归调用dfs对当前遍历值的下一个位置进行判断（上下左右）
        bool res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1)
                    || dfs(board, word, i, j - 1, k + 1) || dfs(board, word, i, j + 1, k + 1);
        //如果四个方向中有一个走得通（即返回true），那就把矩阵中当前位置的字符修改为目标字符串中k指向的相应字符
        //该操作是在最深的一层递归中完成的
        board[i][j] = word[k];

        return res;//向上一层递归返回本层递归结果
    }
public:
    bool exist(vector<vector<char>>& board, string word) {
        //获取矩阵的行列长度
        rows = board.size();
        cols = board[0].size();

        //遍历矩阵
        for(int i = 0; i < rows; ++i){
            for(int j = 0; j < cols; ++j){
                if(dfs(board, word, i, j, 0)) return true;//调用dfs判断目标字符串在矩阵中是否存在,k初始值为0
            }
        }
        return false;
    }
};