LeetCode952三部曲之二：小幅度优化(137ms -＞ 122ms，超39% -＞ 超51%)

欢迎访问我的GitHub

这里分类和汇总了欣宸的全部原创(含配套源码)：https://github.com/zq2599/blog_demos

本篇概览

• 本文是《LeetCode952三部曲》系列之二，在前文中，咱们详细分析了解题思路，然后按照思路写出了代码，在LeetCode提交成功，成绩如下图所示，137ms，超过39%
  
  
• 不得不说这个成绩很不理想，于是今天咱们来尝试进行优化，以减低时间，提升百分比

优化点预判

• 回顾一下题目要求，如下所示
  
  
• 上图中有个重要条件：入参数组中，最大值不超过100000
• 回顾咱们在初始化并查集数据结构的时候，需要满足数组下标代表数字身份这个特性，例如fathers[100000]=123的含义是数字100000的父节点是123，所以数组长度必须是100001，代码如下

int[] fathers = new int[100001];

• 而在实际的并查集操作中，如果入参是4,6,15,35这四个数字，那么fathers这个数组中真正被我们用到的也就只有fathers[4]、fathers[6]、fathers[15]、fathers[35]这四个元素，其他100001-4=99997个元素都没有用到，而代码中还要为这些无用的元素分配空间，还要消耗时间去初始化，这是极大的浪费
• 对于另一个数组rootSetSize，用于记录下标位置元素的子树大小，亦是如此，99997个元素也都浪费了
• 以上就是要优化的地方：如果入参是四个数字，那么fathers和rootSetSize的大小能缩减到四吗？
• 这就需要分析一下了

优化分析

• 先回顾一下解题思路，整个流程如下图所示
  
  

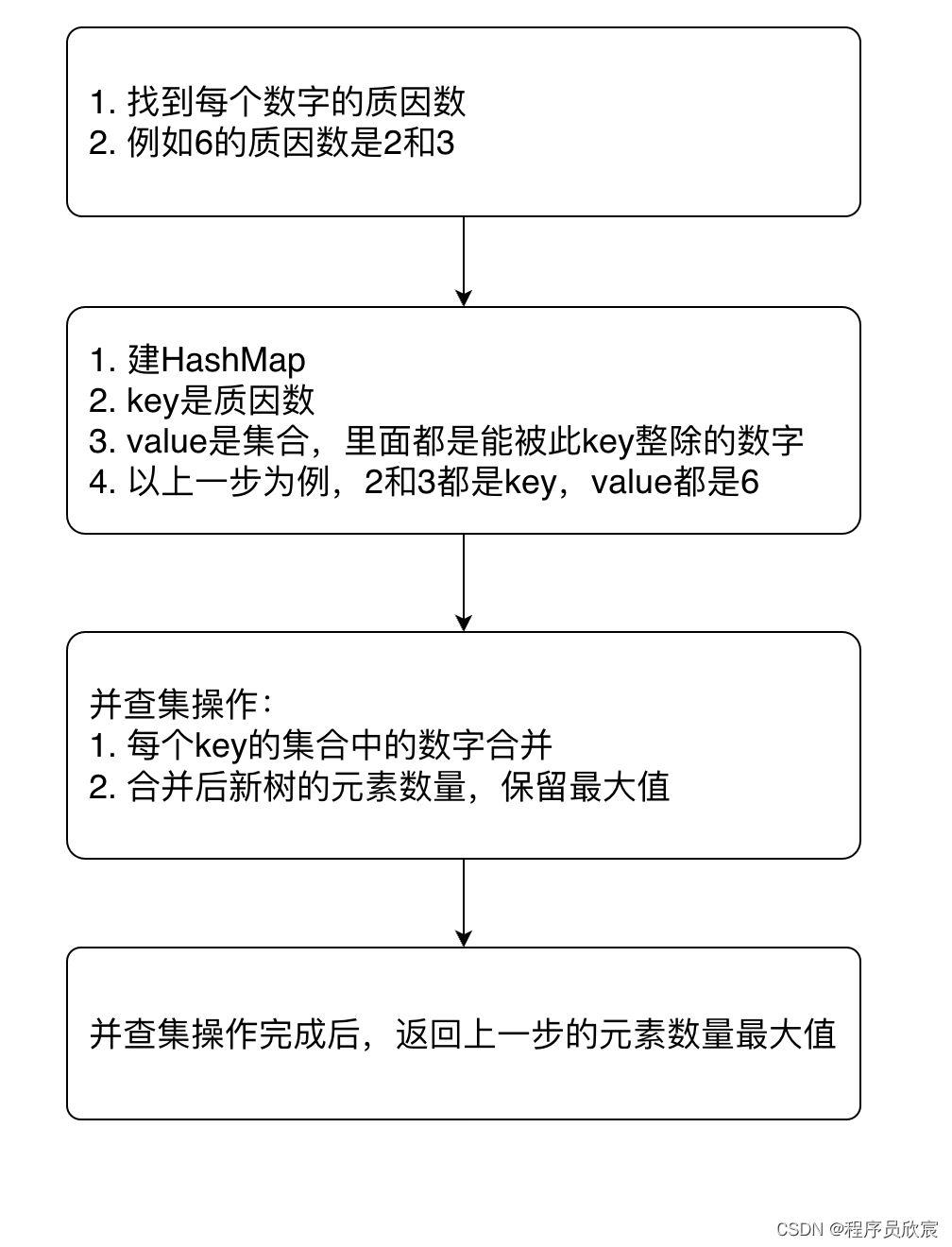
• 假设此题的入参是这四个数字：4，6，15, 35，回顾什么时候咱们会用到这四个数字，显然计算每个数字的质因数的时候必然会用到，计算完成后，得到了下图的关系（这是前文的内容）
  
  

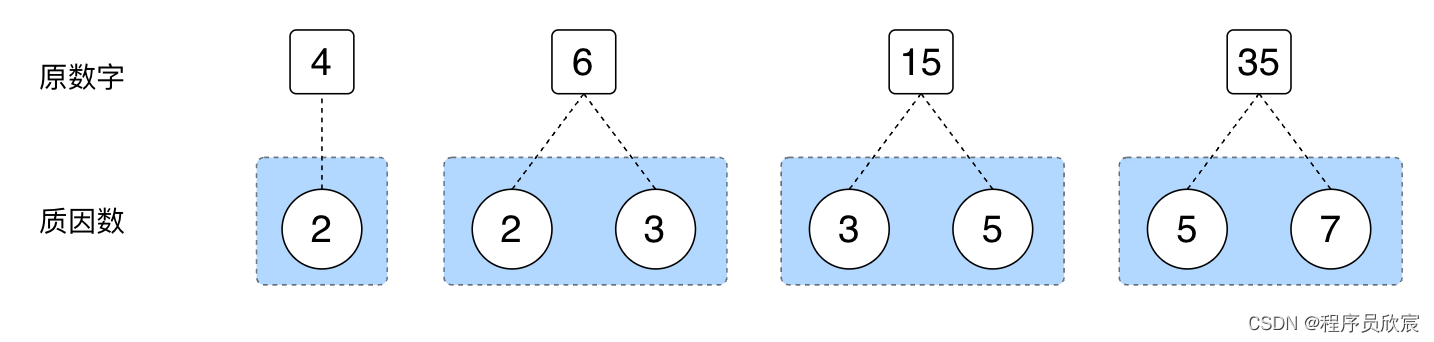
• 然后，咱们根据上图，得到了每个质因数对应的数字集合，也就是下图
  
  

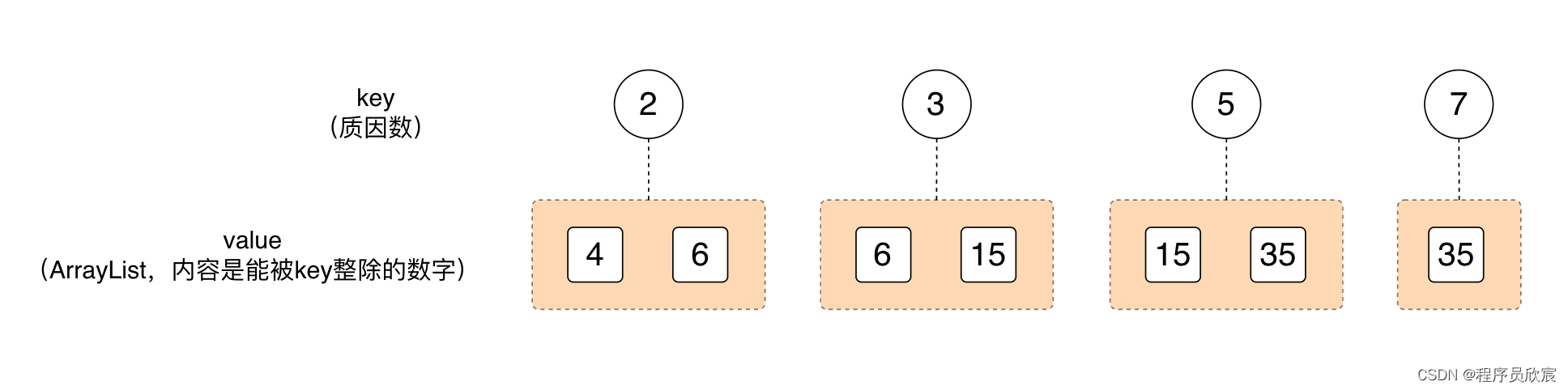
• 看着上图，重点来了：从上图开始，再到后面的并查集操作，再到最终的结束，都不会用4、6、15、35这样的数字去计算什么了

• 所以，上面那幅图中的4、6、15、35，是不是可以替换成他们在入参数组中的下标？假设入参数组是[4,6,15,35]，他们的数组下标就分别是：0、1、2、3

• 将数字替换成数组下标后，上面那幅图的内容就有了变化，变成了下图的样子，之前的[4,6,15,35]四个数字变成了[0,1,2,3]
  
  

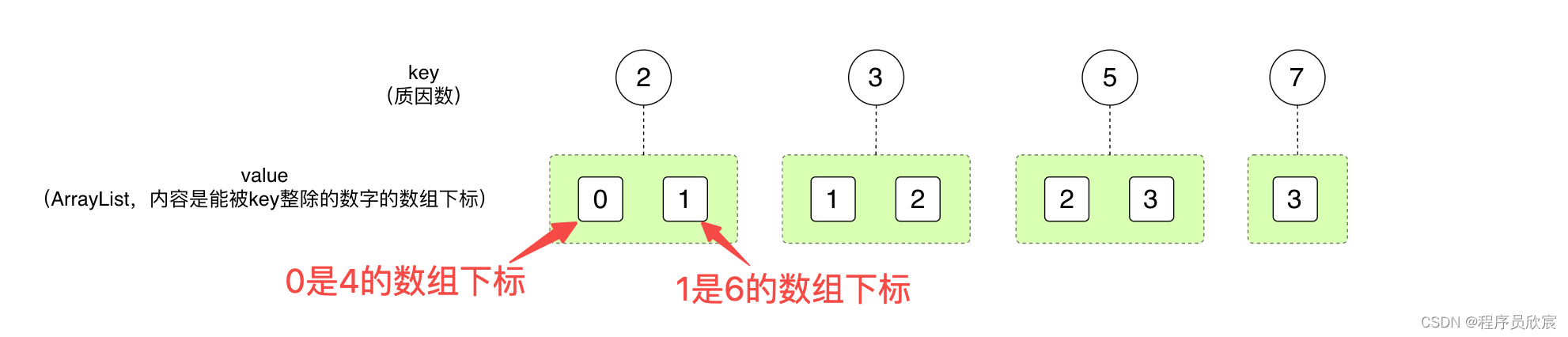
• 接下来的并查集操作中，也可以用[0,1,2,3]取代[4,6,15,35]也可以吗？

• 当然可以，之前是合并4和6，现在变成了合并0和1，题目是要的是连通的数量，而某个唯一的数字到底是4还是它的数组下标0，这不重要了，重要的是合并不能有错就行

• 这样替换后，如果入参是四个数字，不论值是多少，在并查集操作时，只需要用到它们的数组下标：0、1、2、3，最大也只有3

• 这就有意思了，数组fathers和rootSetSize的大小从100001变成了入参数组的长度！

• 准备工作完成了，可以正式动手优化了

优化代码

• 首先，要修改的是定义fathers和rootSetSet的代码，之前是创建固定长度的数组，现在改成先不创建，而是等到后面知道入参数组长度的时候再说
  
  
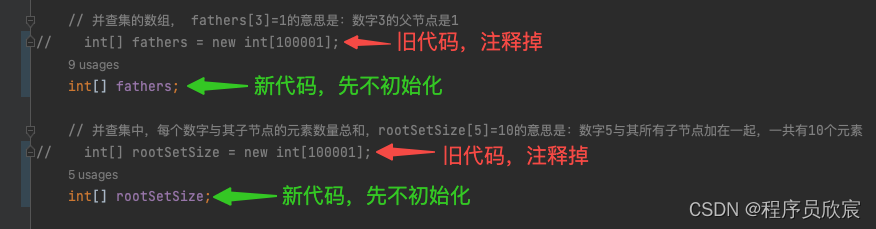
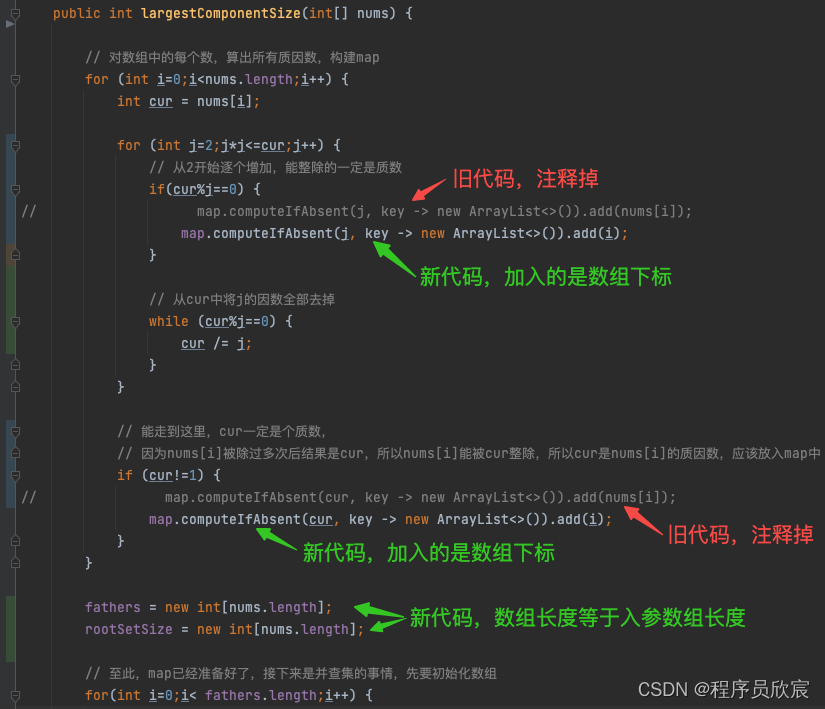
• 然后是largestComponentSize方法中的内容，如下图，存入map的时候，以前存入的是入参的数字，现在传入的是数字对应的数组下标
  
  
• 最后还看到一些代码略有瑕疵，于是顺手改了，如下图，其实影响不大
  
  
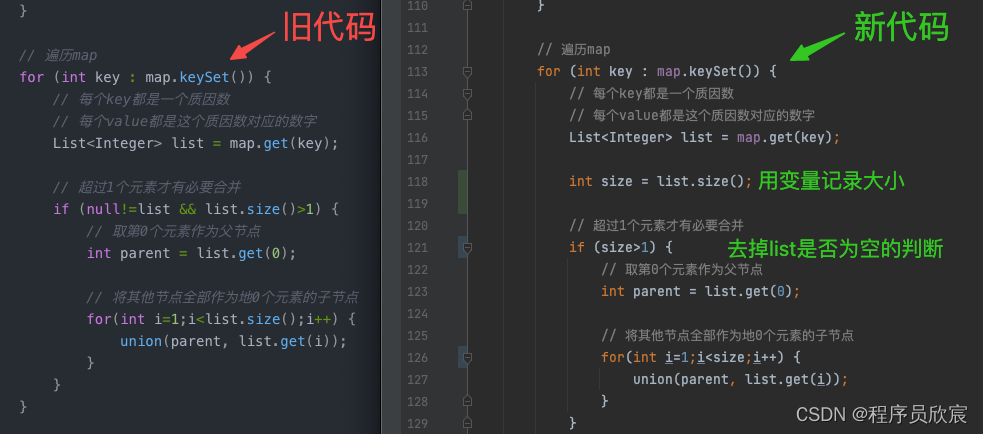
• 以上就是改动的全部了
• 最后附上优化后的完整源码

class Solution {

    // 并查集的数组， fathers[3]=1的意思是：数字3的父节点是1
//    int[] fathers = new int[100001];
    int[] fathers;

    // 并查集中，每个数字与其子节点的元素数量总和，rootSetSize[5]=10的意思是：数字5与其所有子节点加在一起，一共有10个元素
//    int[] rootSetSize = new int[100001];
    int[] rootSetSize;

    // map的key是质因数，value是以此key作为质因数的数字
    // 例如题目的数组是[4,6,15,35]，对应的map就有四个key：2,3,5,7
    // key等于2时，value是[4,6]，因为4和6的质因数都有2
    // key等于3时，value是[6,15]，因为6和16的质因数都有3
    // key等于5时，value是[15,35]，因为15和35的质因数都有5
    // key等于7时，value是[35]，因为35的质因数有7
    Map<Integer, List<Integer>> map = new HashMap<>();

    // 用来保存并查集中，最大树的元素数量
    int maxRootSetSize = 1;

    /**
     * 带压缩的并查集查找(即寻找指定数字的根节点)
     * @param i
     */
    private int find(int i) {
        // 如果执向的是自己，那就是根节点了
        if(fathers[i]==i) {
            return i;
        }

        // 用递归的方式寻找，并且将整个路径上所有长辈节点的父节点都改成根节点，
        // 例如1的父节点是2，2的父节点是3，3的父节点是4，4就是根节点，在这次查找后，1的父节点变成了4，2的父节点也变成了4，3的父节点还是4
        fathers[i] = find(fathers[i]);
        return fathers[i];
    }

    /**
     * 并查集合并，合并后，child会成为parent的子节点
     * @param parent
     * @param child
     */
    private void union(int parent, int child) {
        int parentRoot = find(parent);
        int childRoot = find(child);

        // 如果有共同根节点，就提前返回
        if (parentRoot==childRoot) {
            return;
        }

        // child元素根节点是childRoot，现在将childRoot的父节点从它自己改成了parentRoot，
        // 这就相当于child所在的整棵树都拿给parent的根节点做子树了
        fathers[childRoot] = fathers[parentRoot];

        // 合并后，这个树变大了，新增元素的数量等于被合并的字数元素数量
        rootSetSize[parentRoot] += rootSetSize[childRoot];

        // 更像最大数量
        maxRootSetSize = Math.max(maxRootSetSize, rootSetSize[parentRoot]);
    }

    public int largestComponentSize(int[] nums) {

        // 对数组中的每个数，算出所有质因数，构建map
        for (int i=0;i<nums.length;i++) {
            int cur = nums[i];

            for (int j=2;j*j<=cur;j++) {
                // 从2开始逐个增加，能整除的一定是质数
                if(cur%j==0) {
//                    map.computeIfAbsent(j, key -> new ArrayList<>()).add(nums[i]);
                    map.computeIfAbsent(j, key -> new ArrayList<>()).add(i);
                }

                // 从cur中将j的因数全部去掉
                while (cur%j==0) {
                    cur /= j;
                }
            }

            // 能走到这里，cur一定是个质数，
            // 因为nums[i]被除过多次后结果是cur，所以nums[i]能被cur整除，所以cur是nums[i]的质因数，应该放入map中
            if (cur!=1) {
//                map.computeIfAbsent(cur, key -> new ArrayList<>()).add(nums[i]);
                map.computeIfAbsent(cur, key -> new ArrayList<>()).add(i);
            }
        }

        fathers = new int[nums.length];
        rootSetSize = new int[nums.length];

        // 至此，map已经准备好了，接下来是并查集的事情，先要初始化数组
        for(int i=0;i< fathers.length;i++) {
            // 这就表示：数字i的父节点是自己
            fathers[i] = i;
            // 这就表示：数字i加上其下所有子节点的数量等于1（因为每个节点父节点都是自己，所以每个节点都没有子节点）
            rootSetSize[i] = 1;
        }

        // 遍历map
        for (int key : map.keySet()) {
            // 每个key都是一个质因数
            // 每个value都是这个质因数对应的数字
            List<Integer> list = map.get(key);

            int size = list.size();

            // 超过1个元素才有必要合并
            if (size>1) {
                // 取第0个元素作为父节点
                int parent = list.get(0);

                // 将其他节点全部作为地0个元素的子节点
                for(int i=1;i<size;i++) {
                    union(parent, list.get(i));
                }
            }
        }

        return maxRootSetSize;
    }

}

• 写完代码，提交LeetCode，顺利AC，咱们将优化前和优化后的数据放在一起对比一下，如下图，左边是优化前，右边是优化后，虽然不能算大幅度提升，但勉强算是有明显提升了
  
  
• 至此，第一次优化就完成了，超过50%的成绩依旧很一般，还能进一步提升吗？大幅度提升那种
• 答案自然是可以，感谢咱们这两篇的努力，让我们对解题思路有了深刻理解，接下来，期待第三篇吧，我们会来一次更有效的优化
• 剧透一下：优化点和算素数有关

欢迎访问我的GitHub

这里分类和汇总了欣宸的全部原创(含配套源码)：https://github.com/zq2599/blog_demos

欢迎关注博客园：程序员欣宸

学习路上，你不孤单，欣宸原创一路相伴...