用python将卡尔曼滤波技术和统计套利应用在期货市场

背景

根据当前中国的交易规则，股票不能做空。与更发达的市场相反，套利机会不容易实现。这表明那些寻找并能够利用它们的人可能会有机会。

因此，我决定使用统计套利和配对交易技术专注于中国的期货市场。

战略理念

本项目实施的交易策略称为“统计套利交易”，也称为“配对交易”，是一种逆势策略，旨在从某个配对比率的均值回归行为中获利。

该策略背后的假设是，显示协整特性的对的价差本质上是均值回归，因此如果价差显着偏离均值，将提供套利机会。

数据集

数据集将来自中国金融期货交易所（CFFEX）、上海期货交易所（SHFE）、大连商品交易所（DCE）和郑州商品交易所（ZCE）。

交易策略将进行 678 天的回测（从 2015 年 3 月 30 日到 2017 年 12 月 31 日）。前 542 天（2015 年 3 月 30 日至 2016 年 11 月 14 日占总周期的 80%）为样本内回测期，其余 136 天（15/11/ 2016年至2017年12月31日占总时间的20%）为出样回测期。

中国金融期货交易所（CFFEX）

CFFEX是一家致力于金融[期货]https://bigquant.com/wiki/doc/qihuo-b7SqvngNYn?utm_source=csdn&utm_medium=csdn_article&utm_campaign=20220702_125569227_csdn_article)、期权和其他衍生品交易、清算和结算的股份化交易所。2006年9月8日，经国务院和中国证监会批准，上海期货交易所、郑州商品交易所、大连商品交易所、上海证券交易所、深圳证券交易所在上海设立中金所。

上海期货交易所（SHFE）

上海期货交易所是根据相关规章制度组织的。作为一个自我监管的实体，它履行其章程和国家法律法规中规定的职能。中国证券监督管理委员会（CSRC）对其进行监管。目前，期货合约的标的商品，即

金子，
银，
铜，
铝，
带领，
钢筋，
钢线材，
天然橡胶，
燃油和
锌，上市交易。

大连商品交易所（DCE）

大商所是经国务院批准，受中国证监会监管的期货交易所。多年来，大商所经营有序、稳健发展，已成为全球最大的农产品期货市场和最大的石油、塑料、煤炭、冶金焦、铁矿石期货市场。

它也是中国重要的期货交易中心。截至 2017 年底，大商所共有 16 个期货合约和 1 个期权合约挂牌交易，其中包括

1号大豆，
豆粕，
玉米，
2号大豆，
豆油，
线性低密度聚乙烯（LLDPE），
RBD 棕榈油精，
聚氯乙烯 (PVC),
冶金焦，
焦练煤，
铁矿，
蛋，
纤维板，
细木工板，
聚丙烯（PP），
玉米淀粉期货和
豆粕选项。

郑州商品交易所（ZCE）

郑商所是国务院批准的首个试点期货市场。目前，郑商所上市的产品包括：

小麦（强筋小麦和普通小麦），
早熟长粒粳米，
粳米，
棉布，
油菜籽，
菜籽油，
菜籽粕，
白砂糖，
蒸汽煤，
甲醇，
纯对苯二甲酸 (PTA) 和
平板玻璃。

这些产品构成了涵盖农业、能源、化工和建筑材料等国民经济几个关键领域的综合产品系列。

选择这个特定战略领域的动机

我对中国未来市场的关注主要出于以下几个原因：

首先，由于中国股票市场的不做空限制，我们只能做多股票，这使得与中国股票进行配对交易是不可能的。因为当我们做配对交易时，我们总是做多少数股票而做空相关性高的股票。
更重要的是，在中国未来交易所运作的算法交易公司/策略非常少。我相信这应该提供很好的机会，因为几乎没有竞争。与更发达的市场相反，套利机会并不容易实现，这表明那些寻找并能够利用它们的人可能会有机会。
最后但并非最不重要的一点是，BigQuant 提供了优秀的 API，通过它我可以访问中国四个未来交易所的所有每日主要合约数据。众所周知，高质量的数据在算法交易中起着至关重要的作用。数据的可访问性是我们在选择市场和策略时应该考虑的重要因素之一。

大纲

定义我们的交易品种对，从 BigQuant 下载相关价格数据，并确保为每个交易品种下载的数据长度相同。
每个可能的合约对都将进行协整测试。将执行ADF 测试，使得备择假设是要测试的对是静止的。
对价差运行 Augmented Dickey-Fuller 检验，以统计数据确认该系列是否均值回归。我们还将计算价差系列的赫斯特指数。
对扩展序列和扩展序列的滞后版本运行卡尔曼滤波器回归，然后使用系数计算均值回归的半衰期。
计算交易信号的 Z 分数，定义回测的进出 Z 分数水平。

数据挖掘

访问来自四个期货交易所的每日主要合约数据。

主合约的每日交易价格通过代码列表或者datasource访问

前 542 天（2015 年 3 月 27 日至 2016 年 11 月 14 日占总周期的 80%）为样本内回测期，
其余 136 天（2016 年 11 月 15 日至 2017 年 12 月 29 日占总时间的 20%）为出样回测期。

寻找潜在的交易对

使用样本数据，将执行 ADF 测试，使得备择假设是要测试的对是平稳的。对于p 值 < 0.05，将拒绝零假设。

出去：

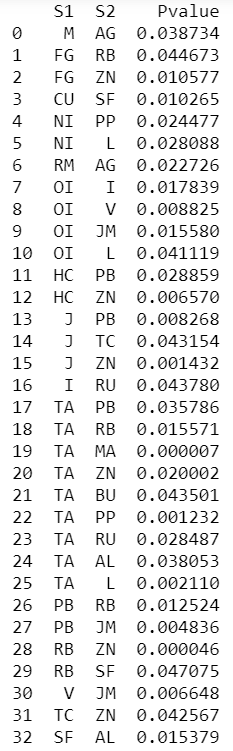
数据分析

交易逻辑

计算每对的点差（点差 = Y – 对冲比率 * X）
使用卡尔曼滤波器回归函数计算对冲比率
使用“半衰期”间隔时间段的滚动平均值和标准偏差计算“s”的 z 分数。将此另存为 z 分数
使用半衰期函数计算半衰期
定义上入口 Z-score = 2.0，下入口 Z-score = 2.0，出口 Z-score = 0.0
当 Z 分数超过 Z 分数上限时，做空；Z-score 平仓 return exit Z-score
当 Z-score 越过较低的入口 Z-score 时，做多；Z-score 平仓 return exit Z-score
对每一对进行回测，并计算性能统计数据，每个数据都以最大值淹没夏普比率
建立市值分布相等的投资组合，每对具有相同的市值

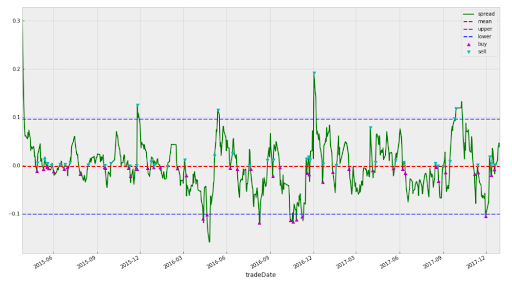
用于动态对冲比率计算的卡尔曼滤波器

根据维基百科，卡尔曼滤波，也称为线性二次估计(LQE)，是一种使用随时间观察到的一系列测量值的算法，包含统计噪声和其他不准确性。

通过估计每个时间范围内变量的联合概率分布，它产生的未知变量估计值往往比仅基于单个测量的估计值更准确。

该过滤器以其理论的主要开发者之一鲁道夫·卡尔曼 (Rudolf E. Kálmán) 的名字命名。

因为卡尔曼滤波器在每个时间步都会更新它的估计值，并且往往比旧的更重视最近的观察结果，所以一个特别有用的应用是对数据的滚动参数的估计。

使用卡尔曼滤波器时，我们不需要指定窗口长度。如果我们感兴趣的话，这对于计算移动平均线很有用，或者对于平滑其他数量的估计很有用。我们已经有了用卡尔曼滤波器计算移动平均和回归的源代码。

赫斯特指数和半衰期

Hurst 指数用于衡量时间序列的长期记忆。它与时间序列的自相关以及随着值对之间的滞后增加而降低的速率有关。

涉及赫斯特指数的研究最初是在水文学中开发的，目的是确定尼罗河长期观察到的多变降雨和干旱条件的最佳大坝尺寸。

“Hurst 指数”或“Hurst 系数”这个名称源自这些研究的首席研究员 Harold Edwin Hurst (1880–1978)；系数的标准符号 H 的使用也与他的名字有关。

为简化起见，这里要记住的重要信息是时间序列可以通过以下方式描述赫斯特指数 (H)：

H < 0.5 - 时间序列是均值回归
H = 0.5 - 时间序列是几何布朗运动
H > 0.5 – 时间序列呈趋势

然而，仅仅因为时间序列显示均值回归特性，并不一定意味着我们可以进行有利可图的交易 - 每周偏离和均值回复的序列与需要 10 年才能均值回复的序列之间存在差异。

我不确定有多少交易者愿意坐下来等待 10 年左右以有利可图的方式结束交易。要了解每次均值回归需要多长时间，我们可以查看时间序列的“半衰期”。

回测

回测引擎遵循以下步骤：

计算点差 = Y – 对冲比率 * X
使用卡尔曼滤波器回归函数计算对冲比率
使用“半衰期”间隔时间段的滚动平均值和标准偏差计算“s”的 z 分数。将此另存为 z 分数
使用半衰期函数计算半衰期
定义上入口 Z-score = 2.0，下入口 Z-score = 2.0，出口 Z-score = 0.0
当 Z 分数超过 Z 分数上限时，做空；Z-score 平仓 return exit Z-score
当 Z-score 越过较低的入口 Z-score 时，做多；Z-score 平仓 return exit Z-score

样本内回测结果

样本内回测时间为 2015 年 2 月 27 日至 2017 年 6 月 15 日。

每个交易对的累计收益

每对的绘制图

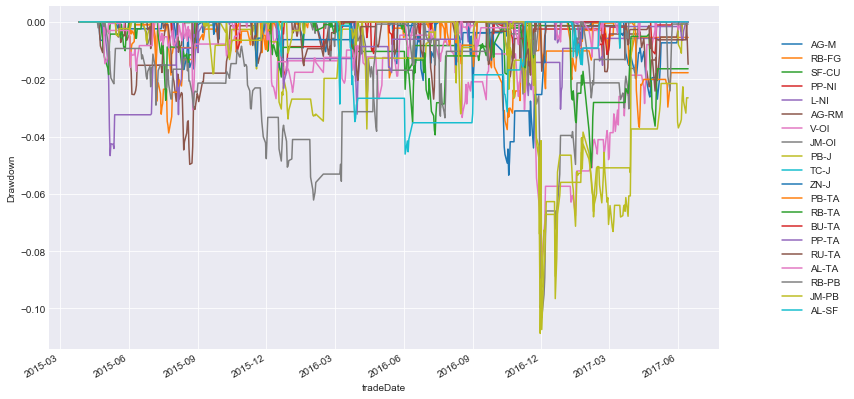
投资组合的样本内回测

投资组合：这是一个等权重的投资组合。

性能统计

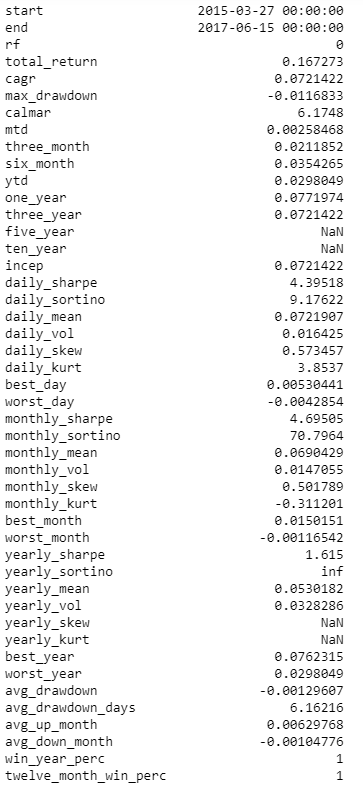
从上表可以看出，投资组合的总回报率为16%，每日夏普比率为4.39。最大跌幅为 1.1%，平均跌幅天数为 6.1。

投资组合的累积回报

投资组合的缩编图

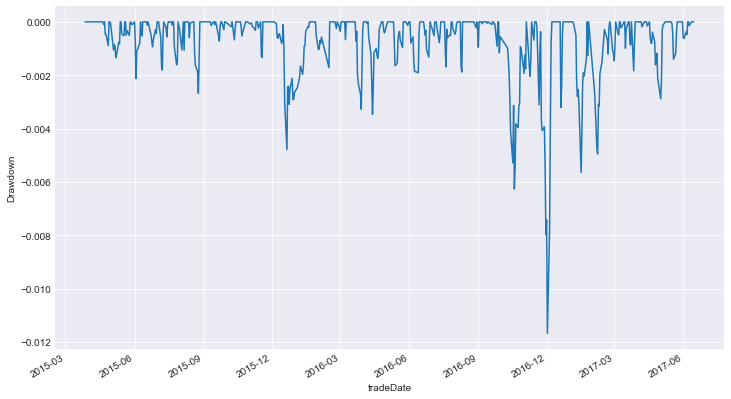
出样回测结果

出样回测时间为 2017/6/16 至 2017/12/31。

每个交易对的累计收益

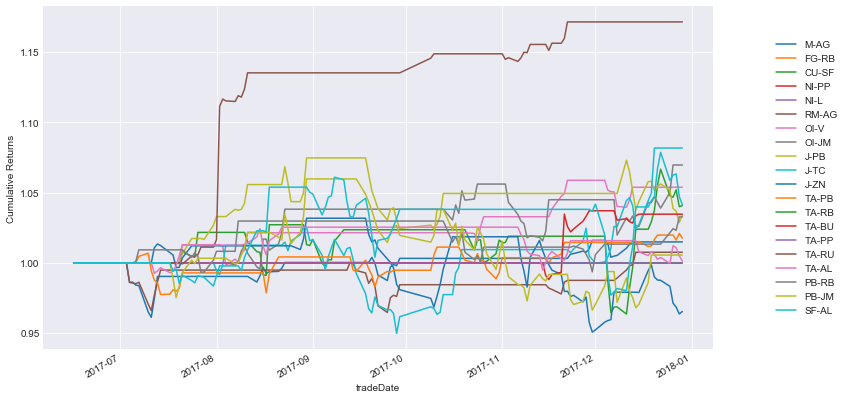
投资组合的累积回报

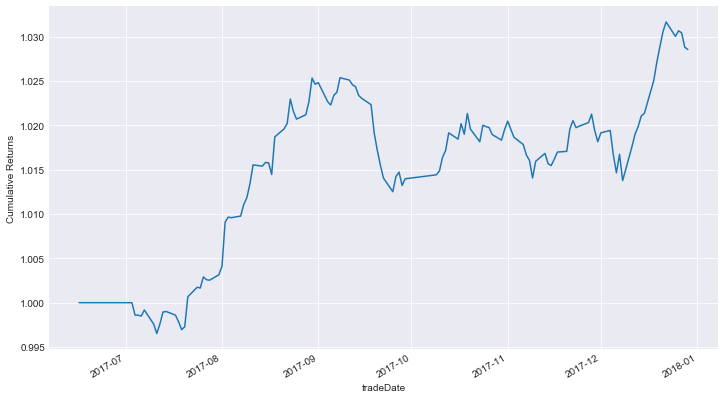
投资组合的业绩统计

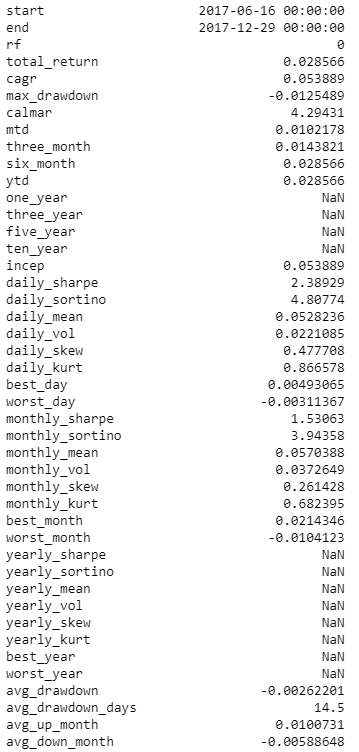
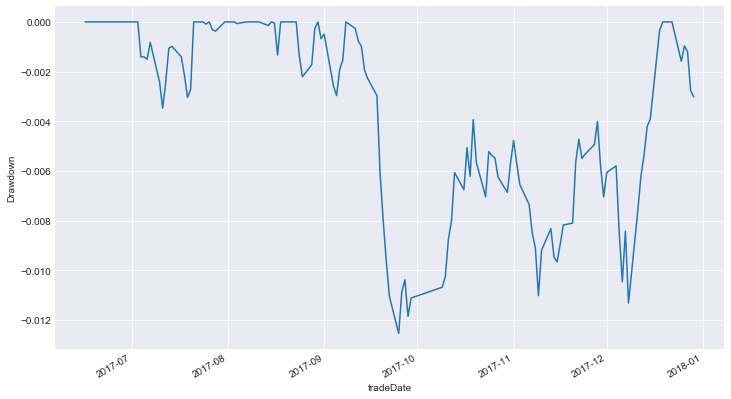
从上表可以看出，投资组合的总回报率为2.8%，每日夏普比率为2.38。最大跌幅为 1.2%，平均跌幅为 14.5。

绘制投资组合图

挑战与局限

进一步的研究可以通过不同入口和出口 z-score 对的模拟次数来测试不同入口和出口 z-score 对的样本内性能，以找到优化 z-score 对
本研究报告基于每日交易数据；可以使用相同的回测引擎来分析分钟数据、小时数据和半数据
回测算法不考虑滑点和交易费用
进一步的研究可以探索其他滤波器，而不仅仅是卡尔曼滤波器
另一个需要优化的窗口是训练周期的长度以及卡尔曼滤波器必须重新校准的频率
回测是基于主力合约数据，在实盘交易中，主力合约应推算到每个月的特殊合约

结论

与更发达的市场相反，套利机会不容易实现，这表明那些寻找并能够利用它们的人可能会有机会。我的项目专注于使用统计套利和配对交易技术的中国期货市场。

该项目对价差运行Augmented Dickey-Fuller 检验，以统计确认序列是否均值回归，计算价差序列的卡尔曼滤波器回归和价差序列的滞后版本，然后使用系数计算一半- 均值回归的寿命。

结果表明，虽然日夏普比率相对较低（2.87 vs. 3.67），但样本外投资组合的预期日回报率较高，并且样本外投资组合的复合年增长率相对较高（0.0858 vs. 0.07882），但平均回撤天数相对较长。

回测算法可用于分析分钟数据、小时数据。主要限制是回测没有考虑滑点和交易费用。