How to Compute The Derivatives （如何求导数）（TBC）

A video by 3Blue1Brown in Bilibili\text{A video by 3Blue1Brown in Bilibili}A video by 3Blue1Brown in Bilibili



I don’t have a systematic face to Derivatives before, but now I do.\text{I don't have a systematic face to Derivatives before, but now I do.}I don’t have a systematic face to Derivatives before, but now I do.

The Derivative of a function is a function which equals to the slope of that\text{The Derivative of a function is a function which equals to the slope of that}The Derivative of a function is a function which equals to the slope of thatfunction’s graph.\text{function's graph.}function’s graph.

1. The Derivative of Power Functions\text{1. The Derivative of Power Functions}1. The Derivative of Power Functions

Let’s look at some simples.\text{Let's look at some simples.}Let’s look at some simples.

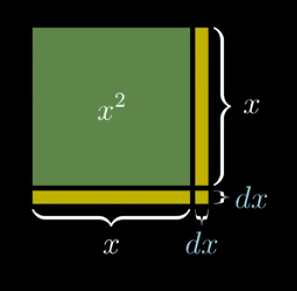
We can treat y=x2 to a square with side length x.\text{We can treat }y=x^2\text{ to a square with side length }x.We can treat y=x2 to a square with side length x.



Let the side length becomes to (x+dx) so that the area increases (2x⋅dx+dx2).\text{Let the side length becomes to }(x+dx)\text{ so that the area increases }(2x·dx+dx^2).Let the side length becomes to (x+dx) so that the area increases (2x⋅dx+dx2).

Because of the increment dx should be much smaller than x, so it’s safe to ignore the\text{Because of the increment }dx\text{ should be much smaller than }x,\text{ so it's safe to ignore the}Because of the increment dx should be much smaller than x, so it’s safe to ignore theterms those have dx2 or high power of dx.\text{terms those have }dx^2\text{ or high power of }dx.terms those have dx2 or high power of dx.

Therefore, ΔS=2x⋅dx. When dx→0,ΔS→2x.\text{Therefore, }\Delta S=2x·dx.\text{ When }dx\rightarrow0,\Delta S\rightarrow 2x.Therefore, ΔS=2x⋅dx. When dx→0,ΔS→2x.

And the same, consider the function y=x3.\text{And the same, consider the function }y=x^3.And the same, consider the function y=x3.

We can treat it to a cube with a side length x.\text{We can treat it to a cube with a side length }x.We can treat it to a cube with a side length x.



Let the side length becomes to (x+dx) so that the volume increases (3x2⋅dx+3x⋅dx2+dx3).\text{Let the side length becomes to }(x+dx)\text{ so that the volume increases }(3x^2·dx+3x·dx^2+dx^3).Let the side length becomes to (x+dx) so that the volume increases (3x2⋅dx+3x⋅dx2+dx3).

As the same, we also let it be 3x2.\text{As the same, we also let it be }3x^2.As the same, we also let it be 3x2.



Actually, for a power function f(x)=xn, it goes\text{Actually, for a power function }f(x)=x^n,\text{ it goes}Actually, for a power function f(x)=xn, it goes

f(x)=xnf(x+dx)=(x+dx)n=xn+nxn−1dx+...f′=Δf=f(x+dx)−f(x)=nxn−1\begin{aligned}f(x)&=x^n\\\\
f(x+dx)&=(x+dx)^n\\
&=x^n+nx^{n-1}dx+...\\\\
f'=\Delta f&=f(x+dx)-f(x)\\
&=nx^{n-1}\end{aligned}f(x)f(x+dx)f′=Δf​=xn=(x+dx)n=xn+nxn−1dx+...=f(x+dx)−f(x)=nxn−1​

Therefore, its dericatives f′=nxn−1.\text{Therefore, its dericatives }f'=nx^{n-1}.Therefore, its dericatives f′=nxn−1.



To be continued.\text{To be continued.}To be continued.