Bitmap简介

1.  BitMap

Bit-map的基本思想就是用一个bit位来标记某个元素对应的Value，而Key即是该元素。由于采用了Bit为单位来存储数据，因此在存储空间方面，可以大大节省。（PS：划重点 节省存储空间）

假设有这样一个需求：在20亿个随机整数中找出某个数m是否存在其中，并假设32位操作系统，4G内存

在Java中，int占4字节，1字节=8位（1 byte = 8 bit）

如果每个数字用int存储，那就是20亿个int，因而占用的空间约为  (2000000000*4/1024/1024/1024)≈7.45G

如果按位存储就不一样了，20亿个数就是20亿位，占用空间约为  (2000000000/8/1024/1024/1024)≈0.233G

高下立判，无需多言

那么，问题来了，如何表示一个数呢？

刚才说了，每一位表示一个数，0表示不存在，1表示存在，这正符合二进制

这样我们可以很容易表示{1,2,4,6}这几个数：

计算机内存分配的最小单位是字节，也就是8位，那如果要表示{12,13,15}怎么办呢？

当然是在另一个8位上表示了：

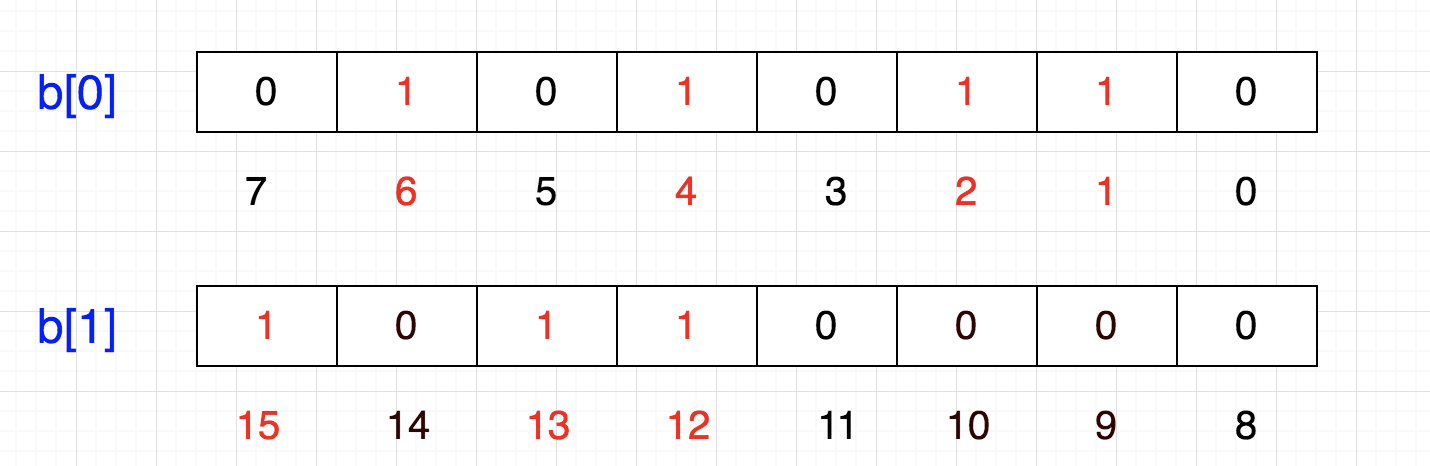
这样的话，好像变成一个二维数组了

1个int占32位，那么我们只需要申请一个int数组长度为 int tmp[1+N/32] 即可存储，其中N表示要存储的这些数中的最大值，于是乎：

tmp[0]：可以表示0~31

tmp[1]：可以表示32~63

tmp[2]：可以表示64~95

。。。

如此一来，给定任意整数M，那么M/32就得到下标，M%32就知道它在此下标的哪个位置

添加 

这里有个问题，我们怎么把一个数放进去呢？例如，想把5这个数字放进去，怎么做呢？

首先，5/32=0，5%32=5，也是说它应该在tmp[0]的第5个位置，那我们把1向左移动5位，然后按位或

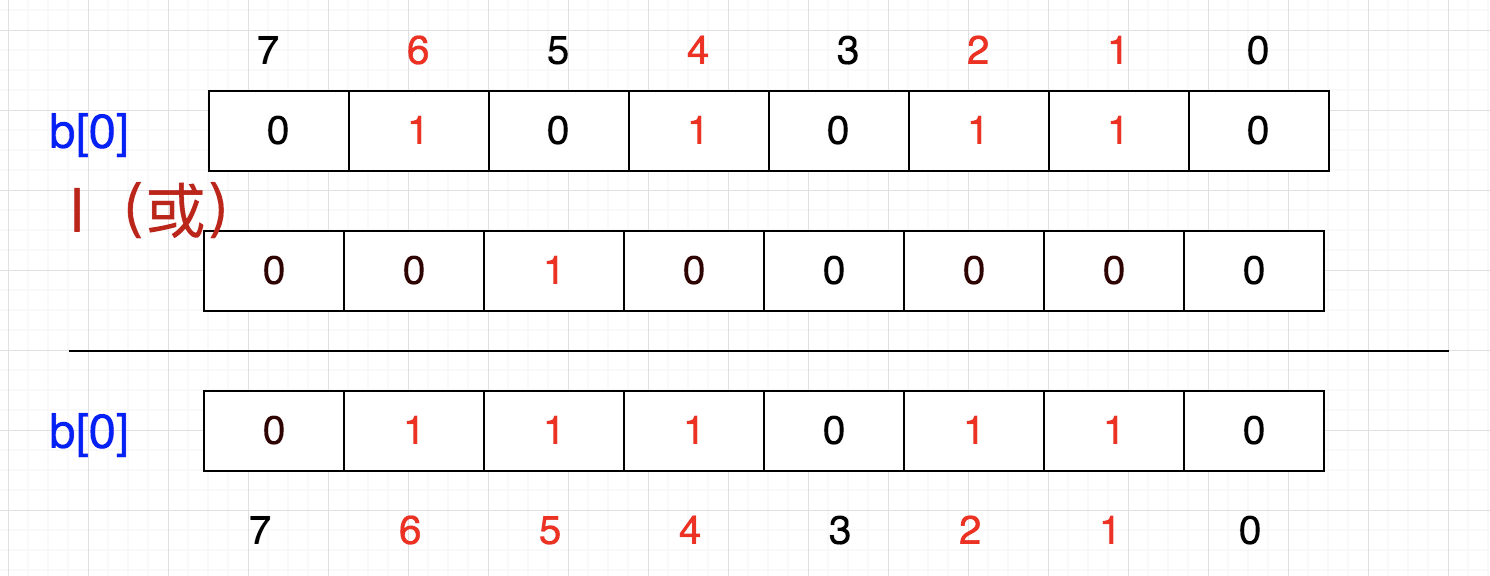
换成二进制就是

这就相当于 86 | 32 = 118

86 | (1<<5) = 118

b[0] = b[0] | (1<<5)

也就是说，要想插入一个数，将1左移带代表该数字的那一位，然后与原数进行按位或操作

化简一下，就是 86 + (5/8) | (1<<(5%8))

因此，公式可以概括为：p + (i/8)|(1<<(i%8)) 其中，p表示现在的值，i表示待插入的数

清除

以上是添加，那如果要清除该怎么做呢？

还是上面的例子，假设我们要6移除，该怎么做呢？

从图上看，只需将该数所在的位置为0即可

1左移6位，就到达6这个数字所代表的位，然后按位取反，最后与原数按位与，这样就把该位置为0了

b[0] = b[0] & (~(1<<6))

b[0] = b[0] & (~(1<<(i%8)))

查找

前面我们也说了，每一位代表一个数字，1表示有（或者说存在），0表示无（或者说不存在）。通过把该为置为1或者0来达到添加和清除的小伙，那么判断一个数存不存在就是判断该数所在的位是0还是1

假设，我们想知道3在不在，那么只需判断 b[0] & (1<<3) 如果这个值是0，则不存在，如果是1，就表示存在

2.  Bitmap有什么用

大量数据的快速排序、查找、去重

快速排序

假设我们要对0-7内的5个元素(4,7,2,5,3)排序（这里假设这些元素没有重复）,我们就可以采用Bit-map的方法来达到排序的目的。

要表示8个数，我们就只需要8个Bit（1Bytes），首先我们开辟1Byte的空间，将这些空间的所有Bit位都置为0，然后将对应位置为1。

最后，遍历一遍Bit区域，将该位是一的位的编号输出（2，3，4，5，7），这样就达到了排序的目的，时间复杂度O(n)。

优点：

• 运算效率高，不需要进行比较和移位；
• 占用内存少，比如N=10000000；只需占用内存为N/8=1250000Byte=1.25M

缺点：

• 所有的数据不能重复。即不可对重复的数据进行排序和查找。
• 只有当数据比较密集时才有优势

快速去重

20亿个整数中找出不重复的整数的个数，内存不足以容纳这20亿个整数。

首先，根据“内存空间不足以容纳这05亿个整数”我们可以快速的联想到Bit-map。下边关键的问题就是怎么设计我们的Bit-map来表示这20亿个数字的状态了。其实这个问题很简单，一个数字的状态只有三种，分别为不存在，只有一个，有重复。因此，我们只需要2bits就可以对一个数字的状态进行存储了，假设我们设定一个数字不存在为00，存在一次01，存在两次及其以上为11。那我们大概需要存储空间2G左右。

接下来的任务就是把这20亿个数字放进去（存储），如果对应的状态位为00，则将其变为01，表示存在一次；如果对应的状态位为01，则将其变为11，表示已经有一个了，即出现多次；如果为11，则对应的状态位保持不变，仍表示出现多次。

最后，统计状态位为01的个数，就得到了不重复的数字个数，时间复杂度为O(n)。

快速查找

这就是我们前面所说的了，int数组中的一个元素是4字节占32位，那么除以32就知道元素的下标，对32求余数（%32）就知道它在哪一位，如果该位是1，则表示存在。

小结&回顾

Bitmap主要用于快速检索关键字状态，通常要求关键字是一个连续的序列（或者关键字是一个连续序列中的大部分）， 最基本的情况，使用1bit表示一个关键字的状态（可标示两种状态），但根据需要也可以使用2bit（表示4种状态），3bit（表示8种状态）。

Bitmap的主要应用场合：表示连续（或接近连续，即大部分会出现）的关键字序列的状态（状态数/关键字个数  越小越好）。

32位机器上，对于一个整型数，比如int a=1 在内存中占32bit位，这是为了方便计算机的运算。但是对于某些应用场景而言，这属于一种巨大的浪费，因为我们可以用对应的32bit位对应存储十进制的0-31个数，而这就是Bit-map的基本思想。Bit-map算法利用这种思想处理大量数据的排序、查询以及去重。

补充1

在数字没有溢出的前提下，对于正数和负数，左移一位都相当于乘以2的1次方，左移n位就相当于乘以2的n次方，右移一位相当于除2，右移n位相当于除以2的n次方。

<< 左移，相当于乘以2的n次方，例如：1<<6   相当于1×64=64，3<<4 相当于3×16=48

>> 右移，相当于除以2的n次方，例如：64>>3 相当于64÷8=8

^  异或，相当于求余数，例如：48^32 相当于 48%32=16

补充2

不使用第三方变量，交换两个变量的值

1 // 方式一
2 a = a + b;
3 b = a - b;
4 a = a - b;
5
6 // 方式二
7 a = a ^ b;
8 b = a ^ b;
9 a = a ^ b;

3.  BitSet

BitSet实现了一个位向量，它可以根据需要增长。每一位都有一个布尔值。一个BitSet的位可以被非负整数索引（PS：意思就是每一位都可以表示一个非负整数）。可以查找、设置、清除某一位。通过逻辑运算符可以修改另一个BitSet的内容。默认情况下，所有的位都有一个默认值false。

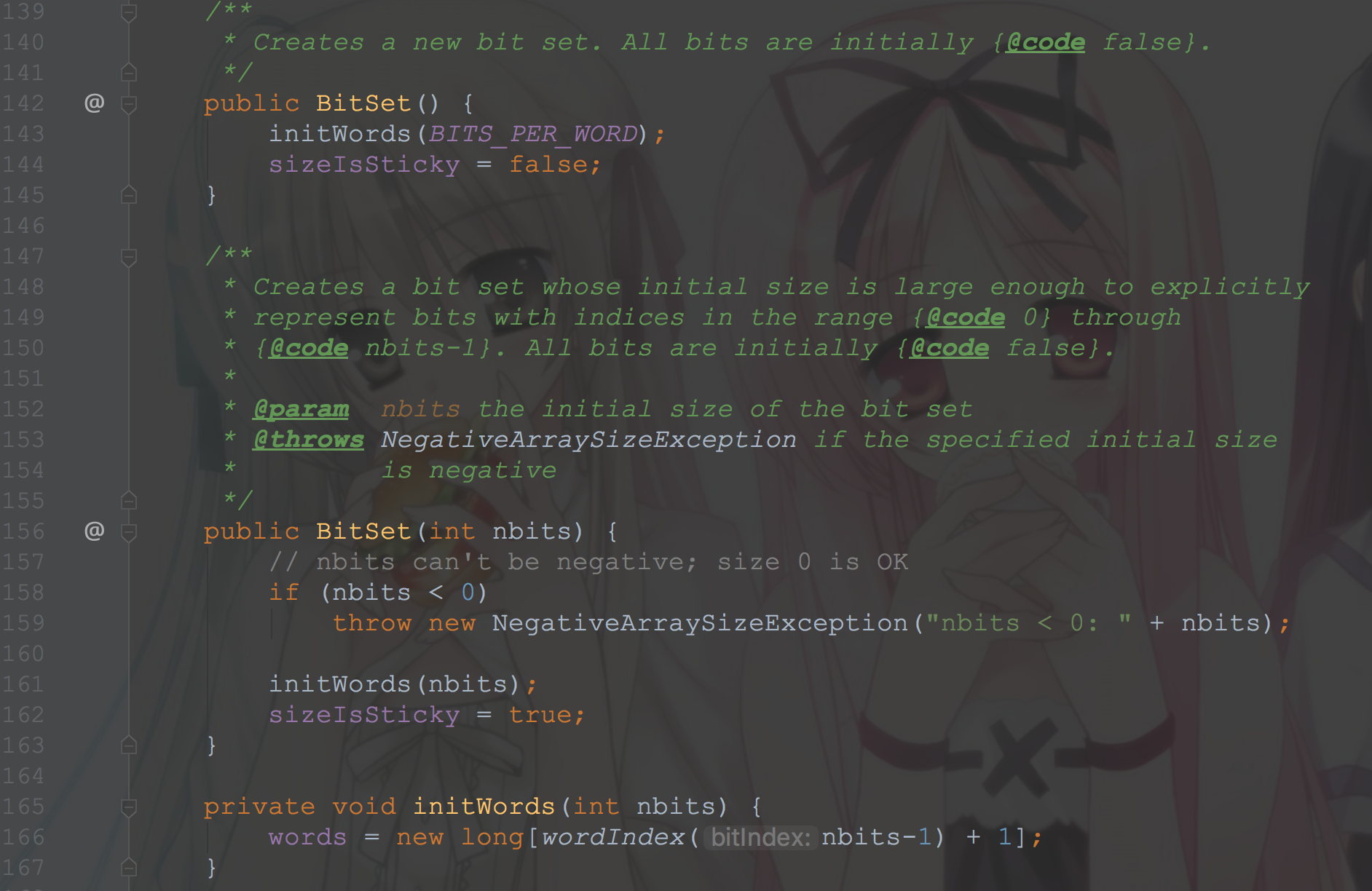
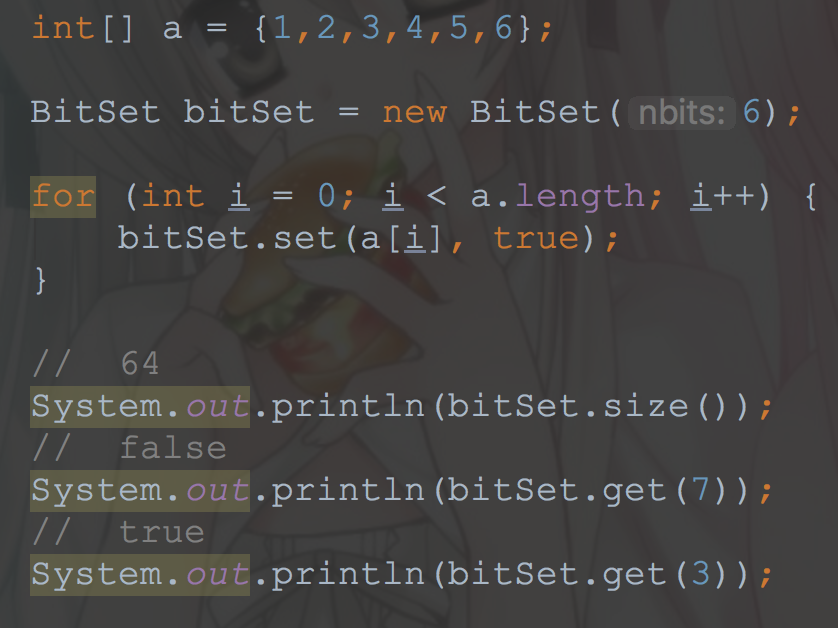
可以看到，跟我们前面想的差不多

用一个long数组来存储，初始长度64，set值的时候首先右移6位（相当于除以64）计算在数组的什么位置，然后更改状态位

别的看不懂不要紧，看懂这两句就够了：

1 int wordIndex = wordIndex(bitIndex);
2 words[wordIndex] |= (1L << bitIndex);

4.  Bloom Filters

Bloom filter 是一个数据结构，它可以用来判断某个元素是否在集合内，具有运行快速，内存占用小的特点。

而高效插入和查询的代价就是，Bloom Filter 是一个基于概率的数据结构：它只能告诉我们一个元素绝对不在集合内或可能在集合内。

Bloom filter 的基础数据结构是一个 比特向量（可理解为数组）。

主要应用于大规模数据下不需要精确过滤的场景，如检查垃圾邮件地址，爬虫URL地址去重，解决缓存穿透问题等

如果想判断一个元素是不是在一个集合里，一般想到的是将集合中所有元素保存起来，然后通过比较确定。链表、树、散列表（哈希表）等等数据结构都是这种思路，但是随着集合中元素的增加，需要的存储空间越来越大；同时检索速度也越来越慢，检索时间复杂度分别是O(n)、O(log n)、O(1)。

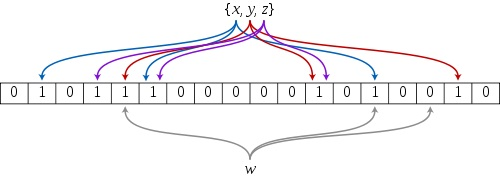
布隆过滤器的原理是，当一个元素被加入集合时，通过 K 个散列函数将这个元素映射成一个位数组（Bit array）中的 K 个点，把它们置为 1 。检索时，只要看看这些点是不是都是1就知道元素是否在集合中；如果这些点有任何一个 0，则被检元素一定不在；如果都是1，则被检元素很可能在（之所以说“可能”是误差的存在）。

BloomFilter 流程

1. 首先需要 k 个 hash 函数，每个函数可以把 key 散列成为 1 个整数；
2. 初始化时，需要一个长度为 n 比特的数组，每个比特位初始化为 0；
3. 某个 key 加入集合时，用 k 个 hash 函数计算出 k 个散列值，并把数组中对应的比特位置为 1；
4. 判断某个 key 是否在集合时，用 k 个 hash 函数计算出 k 个散列值，并查询数组中对应的比特位，如果所有的比特位都是1，认为在集合中。

1 <dependency>
2     <groupId>com.google.guava</groupId>
3     <artifactId>guava</artifactId>
4     <version>28.1-jre</version>
5 </dependenc

com.google.common.hash.BloomFilter

5.  文档

http://llimllib.github.io/bloomfilter-tutorial/zh_CN/

https://www.cnblogs.com/geaozhang/p/11373241.html

https://www.cnblogs.com/huangxincheng/archive/2012/12/06/2804756.html

https://www.cnblogs.com/DarrenChan/p/9549435.html