嵊州D1T4 cf1174E 占梦人

嵊州D1T4 cf1174E

此题为改编题，原题：cf1174E

占梦人

占梦人一个晚上会做 n 个梦，编号为 1 ∼ n，她可以安排做这 n 个梦的顺序。

假如她第一个做了编号为 x 的梦，那么她的初始灵力值就是 x。

接着，如果她在灵力值为 x 的时候 做了编号为 y 的梦，他的灵力值会变成 gcd(x, y)。

只有当灵力值改变时，她才可能预言到一些事情。

她希望能预测到的事情尽量多，那么有多少种安排去做 n 个梦寻找的顺序呢？

请给出答案 %1000000007 的结果。

Input

一行一个整数 n。

Output

一行一个整数表示答案。

Examples

dreams.in	dreams.out
2	1
3	4
6	120
58462	250302017

Notes

对于所有数据，满足 2 ≤ n ≤ 107

Subtask1[28pts]

n ≤ 10

Subtask2[5pts]

n ≤ 13

Subtask3[20pts]

n ≤ 20

Subtask4[26pts]

n ≤ 106

Subtask5[21pts]

无特殊限制

---

Solve！

看到结尾的%1000000007

好熟悉呀！！！

好想翻书！

肯定做过！

好后悔！！！

所以，这告诉我们：

书到用时方恨少！

不瞎扯，继续讲吧！

首先，和上一题一样，先敲一个gcd(a,b)出来嘛。放那里总会有用的！

（光是这个gcd我就调试了10分钟呢。。。）

一定要背牢呀！

（说好不瞎扯的呢？）

咳咳。。。

继续！

int gcd(int x,int y) { return y==?x:gcd(y,x%y);}

口诀：

若y仍然不为零，gcd（y，mod）；

待到y等于零时，返回此时x！

接着！

原题题意

定义gi是排列p1,p2...pi的的GCD（长度为i的前缀GCD）,f(p)是 g1,g2..gn中独特的元素个数

让fmax(n) 成为f(p)在所有整数1,2...n的排列中的最大值，给出整数n，给出满足f(p)=fmax(n)的排列个数 mod(1e9+7)

所以，首个元素s必然有最多的质因数。这样才能在之后n-1次gcd中，获得更多的变化嘛。

每次gcd改变时，只能从其中拿走一个质因数，这样我们可以保证有尽可能多的独特gcd。

解析题目

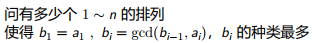
简单的，

因为n比较小

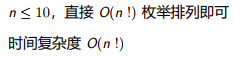
再看看

Subtask2[5pts]

n ≤ 13

我测试了一下，还用原方法会超时的。。。

打表吧？

枚举Subtask

即s只能被2和3整除，因为如果s有其他的质因数p（p>4），我们可以s/p*4，这样可以得到更多质因数。

s=2^x*3^y，即s只能被2和3整除，因为如果s有其他的质因数p（p>4），我们可以s/p*4，这样可以得到更多质因数。

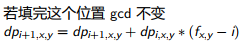
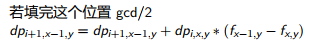
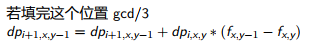
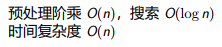
 #include<cstdio>
 #include<algorithm>
 
 using namespace std;
 
 int cal(int x, int y) {return y ? cal(y, x % y) + x / y : x >  ? 1e9 : -;}
 
 int n, i, ans;
 
 int main()
 {
     //freopen("sleepingbeauty.in","r",stdin);
     //freopen("sleepingbeauty.out","w",stdout);
 
     ans = INT_MAX;
     scanf("%d", &n);
     for(int i = ; i <= n; ++i)
         ans = min(ans, cal(n, i));
     printf("%d", ans);
 
     return ;
 }

记得消化！！！！！！！！！！！！！！！