四元数（Quaternion）

从应用角度说一下unity Quaternion，Quaternion是四元数，百度相关资料可能找到的都是一些大牛给你搞个矩阵云云，给你讲解四元数。在此只是从应用角度讲一讲。最简单理解四元数对应一个向量，也可以理解为一个转角，这个取决于应用场合。四元数本身没有特别的含义，就是一个四维向量（不严谨的讲），在不同的情况下代表不同的含义。就像三维向量或者空间坐标（0，0,1),如果说它是坐标就是坐标，如果说是向量就是从零指向（0，0,1)的向量，下面简单说一下quaternion的几种方法。

1） Quaternion.LookRotation()

看文档可以知道这个静态方法有两个重载如下图所示：

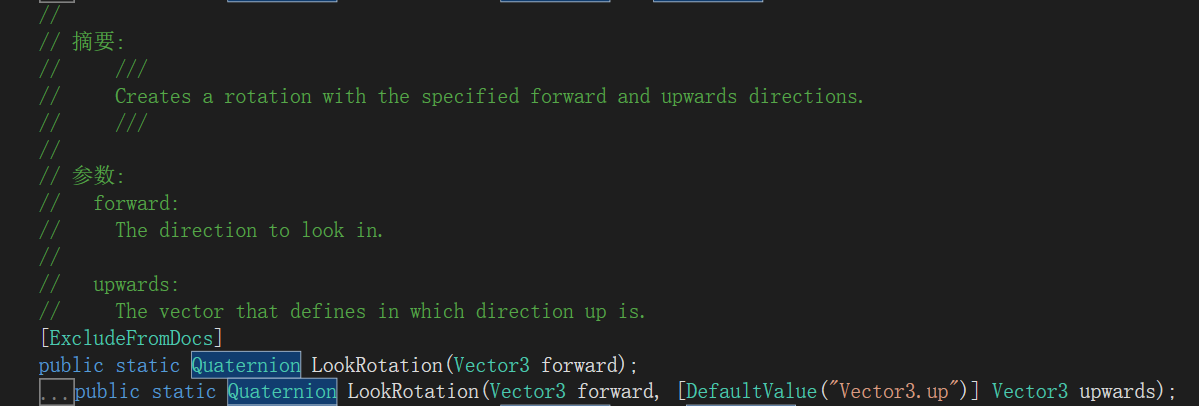
此静态方法的作用是创建一个forwad同向的一个四元数，如果把游戏物体rotation赋值此方法计算结果，则表示游戏物体Z的方向与forward同向

2）Quaternion FromToRotation(Vector3 fromDirection, Vector3 toDirection)

表示通过两个向量计算出一个四元数，这个四元数表示从fromDirection到toDirection旋转，如果转化为三维向量（坐标）则表示从fromDirection到toDirection旋转角度对应的四元数

3）Quaternion operator *(Quaternion lhs, Quaternion rhs)

表示在lhs基础上，再继续转动rhs后的状态