LeetCode 5024 除数博弈 --（简单博弈论）

今天在LeetCode的看到一到题目

这道题目有点坑，没有思路的话容易钻牛角。

刚刚开始时，我想的是直接用while循环来模拟计算，后来觉得这么好麻烦，也有复制的逻辑在里面。后面我推导了一下

以下是我的推导过程，爱丽丝简称 A 鲍勃 简称B

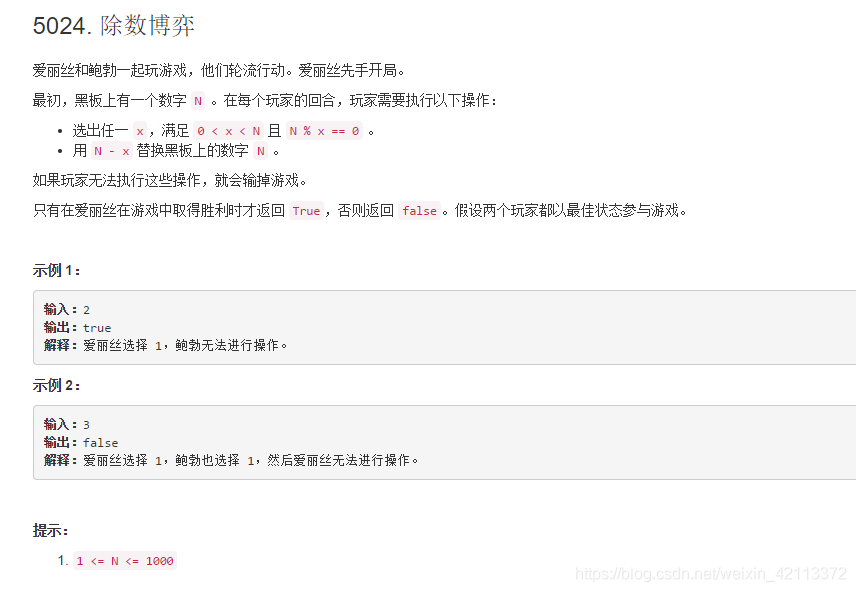
当num=2时，A=1-->num=num-1=1,A赢

当num=3时，A只能出1，-->num=num-1=2，此时B正好处于num=2的情况，所以B可以用之前A的策略，B赢

当num=4时，A可以出1 或 2，但是为了赢，A必须让B处于输的情况，也就是num=3的情况。所以A出1，-->num=num-1=3

当num=5时，A可以出1，-->num=num-1=4,此时B正好处于num=4的情况，B赢

当num=6时，A可以出1，2，3，但是A为了赢，必须让B处于必输的情况下，A出1-->num=num-1,当B出时，num=5，B输。

以此类推，

我们可以得出结论

当N%2==0时，先出的赢

当N%2!=0时，后出的赢

所以这道题目的解为

    public boolean divisorGame(int N) {
        if(N%2==0){
            return true;
        }else{
            return false;
        }
    }

就是这么简单。

我之前还做过另一个类似的题目。

题目好像是：

两个人，轮流报数 1或2 ，然后不停往上加，谁加到30谁就赢。

其实用的是同样的思想。

这种思想和博弈论一样，都是在最理性的情况下进行分析的，

bilibili有好多类似的视频 av7852097 红眼岛岛民自杀事件

海盗分金什么的