Kaldi nnet3的fastlstm与标准LSTM

标准LSTM：

 
 

 
 

 
 

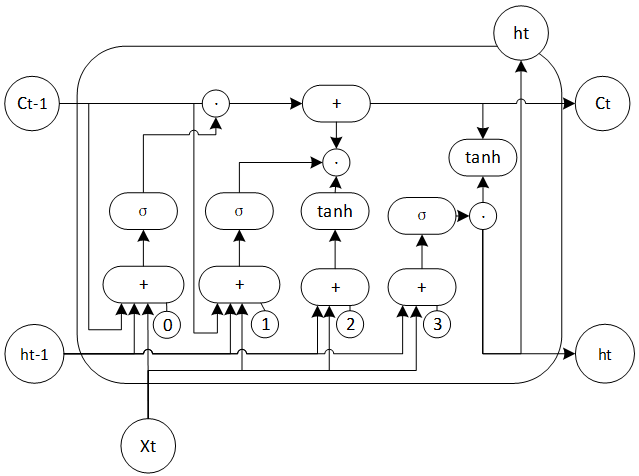
与标准LSTM相比，Kaldi的fastlstm对相同或类似的矩阵运算进行了合并。

 
 

# Component specific to 'projected' LSTM (LSTMP), contains both recurrent and non-recurrent projections

 
 

fastlstm.W_rp, fast lstm Weight recurrent projected

fastlstm.W_all, fast lstm Weight all

fastlstm.rp, fast lstm recurrent projected

同时包含了对循环与非循环的向量的投影

维输入投影为循环的向量维数（如256）与非循环的向量维数（如512）

fastlstm.c, fast lstm cell

fastlstm.m, fast lstm memory

fastlstm.r, fast lstm recurrent

fastlstm.cr_trunc, fast lstm cell recurrent truncate

用于向量的截断，截断为

fastlstm.c_trunc, fast lstm cell truncated

fastlstm.r_trunc, fast lstm recurrent truncated