【子集或者DFS】部分和问题
题目:
给定整数序列a1,a2,...,an,判断是否可以从中选出若干数,使它们的和恰好为k。1≤n≤20 -108≤ai≤108 -108≤k≤108
输入:
n=4
a={1,2,4,7}
k=13
输出:
Yes (13 = 2 + 4 + 7)
思路:
这里记录一下为什么会想到用子集去做这道题目,这道题目是关于从几个数中找出几个关于符合某种关系的数,呐,根据模式匹配法很容易想到这种方法,而关于这种方法也可以推广开来,也就是说只要在n个数据中找几个数据都可以用求子集的方式去做。
代码:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner; public class 部分和 { private static int kk; public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] A = new int[n];
for (int i = 0; i < n; i++) {
A[i] = sc.nextInt();
}
int k = sc.nextInt();// System.out.println("================解法一=============");
ArrayList<ArrayList<Integer>> subsets = getSubsets(A, A.length);
int count = 0;
for (int i = 0; i < subsets.size(); i++) {
for (int j = 0; j < subsets.get(i).size(); j++) {
count += subsets.get(i).get(j); if (count==k&&j==subsets.get(i).size()-1) {
System.out.println("yes k = "+subsets.get(i));
}
}
count = 0; // 如果没找到 要将count置为0
}
// System.out.println(subsets); System.out.println("================解法二=============");
kk = k;
dfs(A, k, 0, new ArrayList<Integer>());
}
/**
* 本题最优解法 二进制求取所有子集然后求和等于k解决问题
*/
public static ArrayList<ArrayList<Integer>> getSubsets(int []A,int n){
Arrays.sort(A); // 正序排序
ArrayList<ArrayList<Integer>> res = new ArrayList<>(); //大集合
for(int i = ex(2, n);i>0;i--){ //大数字-1
ArrayList<Integer> s = new ArrayList<>(); //对每个i建立一个集合
for(int j = n-1;j>=0;j--){ //检查哪个位上的二进制为1,从高位开始检查,高位对应着数组靠后的元素
if(((i>>j)&1)==1){
s.add(A[j]);
}
}
res.add(s);
}
// 生成的结果逆序排序,如果要生成正序排列,很难完成,只有数组反转实现。
return res;
} public static int ex(int a,int n){
if(n==0)return 1;
if(n==1)return a;
int temp = a; // a的1次方
int res = 1;
int exponent = 1;
while((exponent<<1)<n){
temp = temp * temp;
exponent = exponent << 1;
}
res *= ex(a,n-exponent);
return res * temp;
} private static void dfs(int[] a, int k, int cur, ArrayList<Integer> ints) {
if (k == 0) {
System.out.print("Yes (" + kk + " = ");
int size = ints.size();
for (int i = 0; i < size; i++) {
System.out.print(ints.get(i) + (i == size - 1 ? "" : " + "));
}
System.out.println(")");
System.exit(0);
}
if (k < 0 || cur == a.length)
return; dfs(a, k, cur + 1, ints);// 不要cur这个元素 ints.add(a[cur]);
int index = ints.size() - 1;
dfs(a, k - a[cur], cur + 1, ints);
ints.remove(index);// 回溯
}
}
结果:
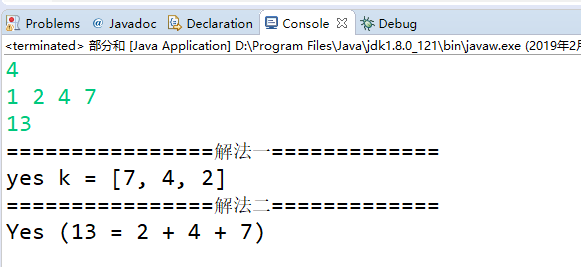
【子集或者DFS】部分和问题的更多相关文章
- [蓝桥杯]2015蓝桥省赛B组题目及详解
/*——————————————————————————————————————————————————————————— [结果填空题]T1 题目:奖券数目 有些人很迷信数字,比如带“4”的数字,认 ...
- COGS 513 八
513. 八 http://www.cogs.pro/cogs/problem/problem.php?pid=513 ★☆ 输入文件:eight.in 输出文件:eight.out 简单 ...
- nyoj 1058部分和问题(DFS)
部分和问题 时间限制:1000 ms | 内存限制:65535 KB 难度:2 描述 给定整数a1.a2........an,判断是否可以从中选出若干数,使它们的和恰好为K. 输入 首先, ...
- 部分和问题(dfs)
部分和问题 时间限制:1000 ms | 内存限制:65535 KB 难度:2 描述 给定整数a1.a2........an,判断是否可以从中选出若干数,使它们的和恰好为K. ...
- 深度优先搜索(DFS)——部分和问题
对于深度优先搜索,这里有篇写的不错的博客:DFS算法介绍 .总得来说是从某个状态开始,不断的转移状态知道无法转移,然后回到前一步的状态.如此不断的重复一直到找到最终的解.根据这个特点,常常会用到递归. ...
- 78. Subsets(中等,集合的子集,经典问题 DFS)
Given a set of distinct integers, nums, return all possible subsets. Note: The solution set must not ...
- POJ-3279.Fliptile(二进制状态压缩 + dfs) 子集生成
昨天晚上12点刷到的这个题,一开始一位是BFS,但是一直没有思路.后来推了一下发现只需要依次枚举第一行的所有翻转状态然后再对每个情况的其它田地翻转进行暴力dfs就可以,但是由于二进制压缩学的不是很透, ...
- UVA 1508 - Equipment 状态压缩 枚举子集 dfs
UVA 1508 - Equipment 状态压缩 枚举子集 dfs ACM 题目地址:option=com_onlinejudge&Itemid=8&category=457& ...
- NYOJ 1058 部分和问题 【DFS】
部分和问题 时间限制:1000 ms | 内存限制:65535 KB 难度:2 描写叙述 给定整数a1.a2........an,推断能否够从中选出若干数.使它们的和恰好为K. 输入 首先,n和k ...
随机推荐
- 插入MongoDB文档:mongo控制台查看插入到MongoDB文档中的内容
const MongoClient = require('mongodb').MongoClient; const assert = require('assert'); const url = 'm ...
- pycharm远程调试服务器
1.下载专业版pycharm并激活 https://blog.csdn.net/weixin_39332299/article/details/79692283 2.创建项目,设置解释器时,选择SSH ...
- Redis的n种妙用,分布式锁,分布式唯一id,消息队列,抽奖……
介绍 redis是键值对的数据库,常用的五种数据类型为字符串类型(string),散列类型(hash),列表类型(list),集合类型(set),有序集合类型(zset) Redis用作缓存,主要两个 ...
- 总zabbix配置-搭建-邮件报警-微信报警-监控mysql
Centos7安装Zabbix4.0步骤 官方搭建zabbix4.0的环境要求: 1. 环境搭建LAMP 前提Centos系统安装完成: 确认一下: 1 2 cat /etc/redhat-rele ...
- Postman测试上传文件
postman测试上传文件 输入url:http://127.0.0.1:8081/uploadfile 选择post方式 选择body 选择form-data,text改为file 输入key: ...
- Aspnet Core 对 Resetful API版本的支持
在实际项目过程中API往往会收到迭代的影响,同时具备多个版本,因此resetful接口的版本话是非常重要的. 其实官方就提供了很好的支持,微软爸爸在nuget提供了Microsoft.AspNetCo ...
- IntelliJ IDEA 2018.3.3配置 Tomcat 9,控制台出现中文乱码 “淇℃伅”(2019/01/25)
(win10系统) 全新idea配置全新版本Tomcat突遇 “淇℃伅”,网上大部分解决方案均已失效 似乎是idea与Tomcat命令行输出格式不一致所致,千辛万苦在某一小角落发现这个方法,一针见血, ...
- redis对键进行的相关操作
redis对键操作的相关命令以及如何在python使用这些命令 redis对键操作的命令: 命令 语法 概述 返回值 Redis DEL 命令 del key [key ...] 该命令用于在 key ...
- POJ 3268 (dijkstra变形)
题目链接 :http://poj.org/problem?id=3268 Description One cow from each of N farms (1 ≤ N ≤ 1000) conveni ...
- angular之表达式
1.作用:使用表达式把数据绑定到HTML. 2.语法:表达式写在双打括号内:{{expression}} 3.比较:表达式作用类似于ng-bind指令:建议更多的使用指令. 4.AngularJS表达 ...
