Codeforces Round #530 (Div. 2) C D

C：

*可以保留删除或者增加

？ 保留或者删除

#include<bits/stdc++.h>
using namespace std;
int main(){
    string s;
    int k,len;
    cin>>s>>k;
    ;
    len = s.size();
    ;j<len;j++){
        if(isalpha(s[j])) sumx++;
        else sumx--;
    }
    if(sumx>k){
        cout<<"Impossible"<<endl;
    }else{
       string ans = "";
       int sum = k-sumx;
       ;j<len-;j++){
          ])){
             ans+=s[j];
          }else{
             ] == '?'){
                if(sum){
                   sum--;
                   ans+=s[j];
                }
             }] == '*'){
                while(sum){
                    sum--;
                    ans+=s[j];
                }
             }
          }
       }
       ])){
          ans+=s[len-];
       }
       if(ans.size()==k) cout<<ans<<endl;
       else{
         cout<<"Impossible"<<endl;
       }
    }
    ;
}

D:

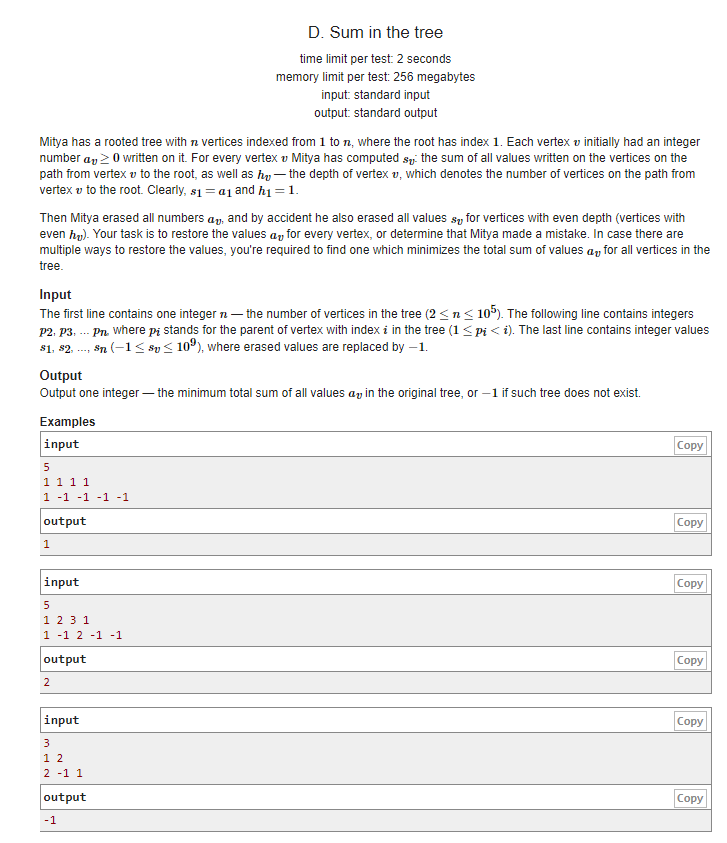
把深度为偶数的节点隐藏掉（-1） 给出每个节点的父亲以及这个点到 根部的 value值总和 包括自己在内  求这棵树最小的value总和

#include<bits/stdc++.h>
using namespace std;
#define maxn 100005
#define inf 99999999999999
#define LL long long
#define debug(x) cout<<x<<endl
vector<LL>q[maxn];
LL a[maxn],ans[maxn],va=;
;
void dfs(LL u,LL fa,LL deep){
   ==){
      LL mi = inf;
      ;j<q[u].size();j++){
         mi = min(mi,a[q[u][j]]);
      }
      if(mi==inf){
         ans[u] = ;
         a[u] = a[fa];
      }else{
         a[u] = mi;
         ans[u] = a[u] - a[fa];
      }
   }else{
      ){
         ans[u] = a[u] - a[fa];
      }
   }
   ;j<q[u].size();j++){
      int v = q[u][j];
      dfs(v,u,deep+);
   }
}
int main(){
    LL n;
    scanf("%lld",&n);
    ;j<=n;j++){
        LL x;
        scanf("%d",&x);
        q[x].push_back(j);
    }
    ;j<=n;j++){
        scanf("%lld",&a[j]);
    }
    ans[]=a[];
    dfs(,,);
    ;j<=n;j++){
        va+=ans[j];
        //cout<<ans[j]<<endl;
        ){
            cout<<"-1"<<endl;
            ;
        }
    }
    cout<<va<<endl;
}