bzoj5286 [Hnoi2018]转盘

题目描述：

bz

luogu

题解：

看了半个晚上终于明白了。

首先最优决策一定有：在起始点停留一段时间然后一直前进。

解释网上有很多，在这里不赘述了。

（由于是环，先把$T$数组倍长。）

首先基于决策我们的答案是$n-1+min_{i=1}^{n}i+max_{j=i}^{i+n-1}T[j]-j$

考虑到$i+n-1$的后面一定不会有$max$，我们可以把上式变成$n-1+min_{i=1}^{n}i+max_{j=i}^{2*n}T[j]-j$

那么右面那个的形式可以看做$min_{i=l}^{mid}i+max_{j=i}^{r}A[j]$，其中$A[j]=T[j]-j$

那么设$t[u]$等于上面这个是式子，$mx[u]=max_{i=l}^{r}A[i]$。

所以差不多是这个形状：

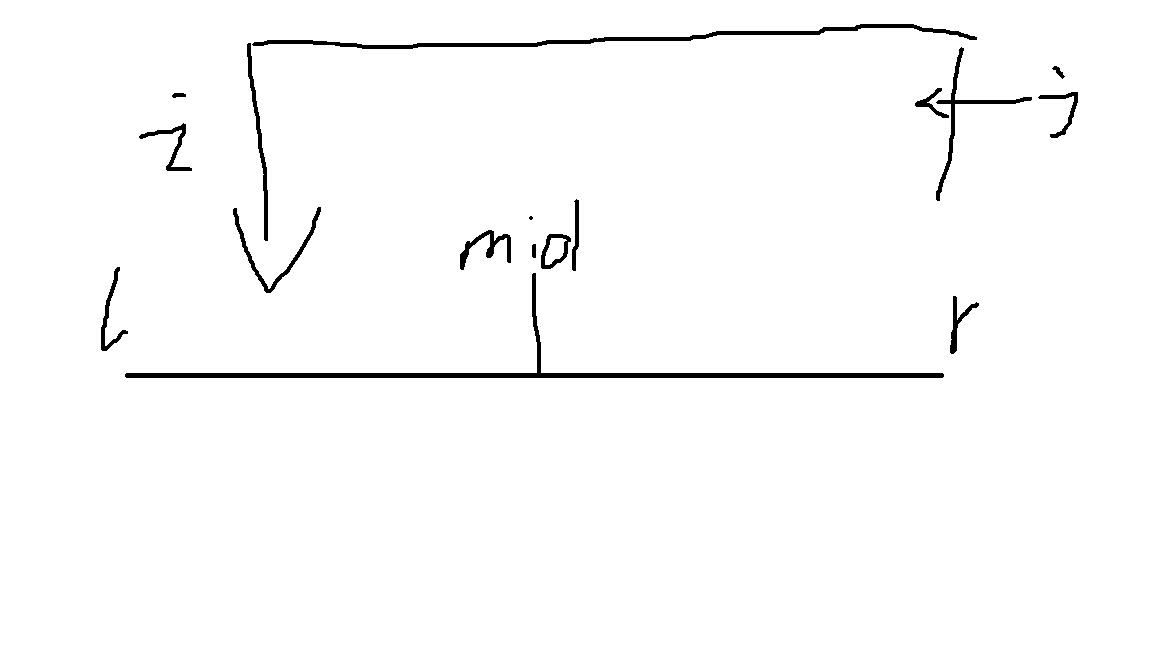
显然$mx[u]$可以从下往上$O(1)$转移。

至于$t$即答案数组，由于我们有线段树，所以在线段树上分治搞下去。

具体按$i$指向左边一半的左边还是右边讨论，两者取$min$。

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = ;
template<typename T>
inline void read(T&x)
{
    T f = ,c = ;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){c=c*+ch-'';ch=getchar();}
    x = f*c;
}
int n,m,op,T[N<<],ans;
struct segtree
{
    int t[N<<],mx[N<<];
    int query(int l,int r,int u,int bas)
    {
        if(l==r)return l+max(bas,mx[u]);
        int mid = (l+r)>>;
        if(bas<=mx[u<<|])return min(query(mid+,r,u<<|,bas),t[u]);
        else return min(query(l,mid,u<<,bas),mid++bas);
    }
    void update(int l,int r,int u)
    {
        int mid = (l+r)>>;
        t[u] = query(l,mid,u<<,mx[u<<|]);
        mx[u] = max(mx[u<<],mx[u<<|]);
    }
    void build(int l,int r,int u)
    {
        if(l==r){t[u]=T[l],mx[u]=T[l]-l;return ;}
        int mid = (l+r)>>;
        build(l,mid,u<<);
        build(mid+,r,u<<|);
        update(l,r,u);
    }
    void insert(int l,int r,int u,int qx)
    {
        if(l==r){t[u]=T[l],mx[u]=T[l]-l;return ;}
        int mid = (l+r)>>;
        if(qx<=mid)insert(l,mid,u<<,qx);
        else insert(mid+,r,u<<|,qx);
        update(l,r,u);
    }
}tr;
int main()
{
    read(n),read(m),read(op);
    for(int i=;i<=n;i++)
        read(T[i]),T[i+n]=T[i];
    tr.build(,*n,);
    printf("%d\n",ans=tr.t[]+n-);
    for(int x,y,i=;i<=m;i++)
    {
        read(x),read(y);
        if(op)x^=ans,y^=ans;
        T[x] = y,T[x+n] = y;
        tr.insert(,*n,,x);tr.insert(,*n,,x+n);
        printf("%d\n",ans=tr.t[]+n-);
    }
    return ;
}