P1382 楼房 (扫描线,线段树)

题目描述

地平线(x轴)上有n个矩(lou)形(fang)，用三个整数h[i],l[i],r[i]来表示第i个矩形：矩形左下角为(l[i],0)，右上角为(r[i],h[i])。地平线高度为0。在轮廓线长度最小的前提下，从左到右输出轮廓线。

下图为样例2

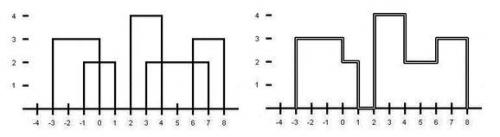
输入输出格式

输入格式：

第一行一个整数n，表示矩形个数

以下n行，每行3个整数h[i],l[i],r[i]表示第i个矩形。

输出格式：

第一行一个整数m，表示节点个数

以下m行，每行一个坐标表示轮廓线上的节点。从左到右遍历轮廓线并顺序输出节点。第一个和最后一个节点的y坐标必然为0。

输入输出样例

输入样例#1：

【样例输入1】
2
3 0 2
4 1 3

【样例输入2】
5
3 -3 0
2 -1 1
4 2 4
2 3 7
3 6 8

输出样例#1：

【样例输出1】
6
0 0
0 3
1 3
1 4
3 4
3 0

【样例输出2】
14
-3 0
-3 3
0 3
0 2
1 2
1 0
2 0
2 4
4 4
4 2
6 2
6 3
8 3
8 0

说明

【数据范围】

对于30%的数据，n<=100

对于另外30%的数据，n<=100000,1<=h[i],l[i],r[i]<=1000

对于100%的数据，1<=n<=100000,1<=h[i]<=10^9,-10^9<=l[i]<r[i]<=10^9

思路

1.扫描线:

先把每个矩形拆成两条边,一条入边,一条出边,然后按照横坐标以及高度排序,同时还需要一个堆实时记录高度,然后一遍从左到右的遍历就可以求出每个交点和交点的个数,然后即可解.

2.离散化+线段树

（贼麻烦）...

上代码

#include<bits/stdc++.h>
using namespace std;
const int maxn=;
int read()
{
    char ch=getchar();int f=,w=;
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch<=''&&ch>=''){w=w*+ch-'';ch=getchar();}
    return f*w;
}

struct ls{
    int up;
    int x;
    int k;
}l[maxn];

struct ss{
    int ax;
    int ay;
}ans[maxn*];
int n,cnt,num;
multiset<int>s;

int cmp(ls i,ls j)
{
    if(i.x!=j.x)return i.x<j.x;
    if(i.k!=j.k)return i.k<j.k;
    if(i.k==)return i.up>j.up;
    if(i.k==)return i.up<j.up;
}

int main(){
    n=read();
    for(int i=;i<=n;i++){
        int h,ll,r;
        h=read(),ll=read(),r=read();
        l[++cnt].up=h; l[cnt].x=ll;l[cnt].k=;
        l[++cnt].up=h; l[cnt].x=r,l[cnt].k=;
    }
    sort(l+,l+cnt+,cmp);
    s.insert();
    for(int i=;i<=cnt;i++){
        int mx=*s.rbegin();
        if(l[i].k==){
            if(l[i].up<=mx) s.insert(l[i].up);
            else{
                ++num;ans[num].ax=l[i].x;ans[num].ay=mx;
                ++num;ans[num].ax=l[i].x;ans[num].ay=l[i].up;
                s.insert(l[i].up);
            }
        }
        if(l[i].k==){
            if(l[i].up==mx&&s.count(mx)==){
                s.erase(mx);
                ans[++num].ax=l[i].x; ans[num].ay=l[i].up;
                ans[++num].ax=l[i].x;ans[num].ay=*s.rbegin();
            }
            else s.erase(s.find(l[i].up));
        }
    }
    printf("%d\n",num);
    for(int i=;i<=num;i++)
   cout<<ans[i].ax<<' '<<ans[i].ay<<endl;
    return ;
}