要让苹果App在真机上跑，需要私钥(PrivateKey)，证书(Certificate)和描述文件(Provisioning Profile)。

(一) 安全基础：

　　1.非对称加密：

　　

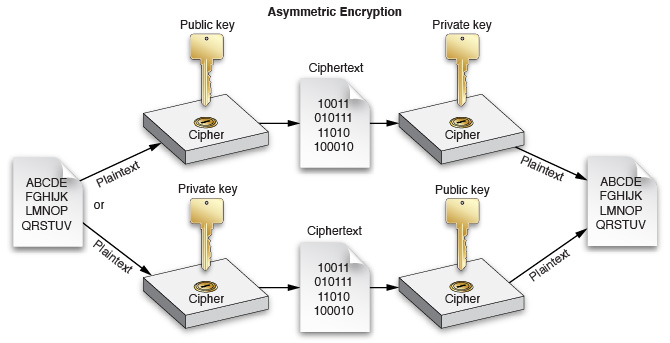
　　2.Hash码

(二) CodeSign

　　打包app上传的时候，为了确保在传输过程中app内容没有被更改，需要一种验证机制，传输之前会用对整个app包进行hash算法计算得到一串hash码，再用私钥对这串hash码加密。在打包上传的时候我们需要提供一个证书，证书里面包含该私钥对应的公钥，上传到苹果那边之后他们用公钥解密之前加密的hash码，然后对比加密前和解密后的hash码，如果一样，则表示app包在传输过程中没有被改变。上传的证书在申请的时候也被苹果签名，证书包括公钥和作者或公司的一些信息，在证书的扩展里面也描述了证书的用途，比如一个用来验证签名过的邮件信息的证书是不能用来验证签名过的可执行代码。

　　

(三) Provisioning Profile

　　Provisioning 是准备和配置应用程序在设备上启动和使用应用程序服务的过程。在开发的时候，你选择哪些设备可以运行您的 iOS 应用程序，哪些应用程序服务你的 iOS 和 Mac 的应用程序可以访问。
provisioning profile 是从会员中心下载并被包含在app包里面。如果provisioning profile中的信息不符合特定条件，您的应用程序不会启动。

　　eg:TeamProfile

　　

　　

CodeSign相关的更多相关文章

  1. 嵌入式单片机STM32应用技术（课本）

    目录SAIU R20 1 6 第1页第1 章. 初识STM32..................................................................... ...

  2. iOS-开发者相关的几种证书

    目录 引言 写在前面 一App IDbundle identifier 二设备Device 三开发证书Certificates 证书的概念 数字证书的概念 iOS开发证书 iOS开发证书的根证书 申请 ...

  3. 【IOS打包】ARCHIVE FAILED：Command CodeSign failed with a nonzero exit code

    [问题] [解决办法] 用xcode打开项目 command + k 重启电脑 参照:xcode打包报错command codesign failed with a nonzero exit code ...

  4. Xcode相关

    Xcode相关的路径 Provisioning Profiles存放路径:~/Library/MobileDevice/Provisioning Profiles 所有模拟器(包括历史模拟器):~/L ...

  5. java中的字符串相关知识整理

    字符串为什么这么重要 写了多年java的开发应该对String不陌生,但是我却越发觉得它陌生.每学一门编程语言就会与字符串这个关键词打不少交道.看来它真的很重要. 字符串就是一系列的字符组合的串,如果 ...

  6. SQL Server相关书籍

    SQL Server相关书籍 (排名不分先后) Microsoft SQL Server 企业级平台管理实践 SQL Server 2008数据库技术内幕 SQL Server性能调优实战 SQL S ...

  7. dotNET跨平台相关文档整理

    一直在从事C#开发的相关技术工作,从C# 1.0一路用到现在的C# 6.0, 通常情况下被局限于Windows平台,Mono项目把我们C#程序带到了Windows之外的平台,在工作之余花了很多时间在M ...

  8. 在ASP.NET Core应用中如何设置和获取与执行环境相关的信息？

    HostingEnvironment是承载应用当前执行环境的描述,它是对所有实现了IHostingEnvironment接口的所有类型以及对应对象的统称.如下面的代码片段所示,一个HostingEnv ...

  9. virtualbox linux虚拟机相关

    linux虚拟机设置为静态IP 在virtualbox中安装好linux虚拟机后,如果采用的是NAT方式的话,linux虚拟机默认采用dhcp方式自动上网,而且用的是NetworkManager服务而 ...

随机推荐

  1. perfect-scrollbar 轻量级滚动插件

    它是一个轻量级的jquery插件. 需要引入的文件: css: #box { position: absolute; overflow: hidden; height: 200px; width: 2 ...

  2. Codeforces Gym101502 K.Malek and Summer Semester

    K. Malek and Summer Semester   time limit per test 1.0 s memory limit per test 256 MB input standard ...

  3. (五）github删除仓库

    一.一直学习怎么创建仓库,创建了太多仓库,一直不知道咋删除,有点懵,其实很简单,就是对英文不太习惯,要加深英文水平. 找到setting,然后再下面找到danger Zone

  4. android 扩大view的响应区域

    1.Android提供TouchDelegate帮助实现扩大一个很小的view的点击区域 例如:https://developer.android.com/training/gestures/view ...

  5. MySql----on duplicate key

    mysql on duplicate key 语句是解决key 冲突的问题,同时 ,key 包括 primary key 和 unique key 等

  6. Oracle 实例名/服务名 请问SID和Service_Name有什么区别

    可以简单的这样理解:一个公司比喻成一台服务器,数据库是这个公司中的一个部门. 1.SID:一个数据库可以有多个实例(如RAC),SID是用来标识这个数据库内部每个实例的名字, 就好像一个部门里,每个人 ...

  7. maven运行update命令时报org/apache/maven/shared/filtering/MavenFilteringException错误

           在eclipse中对准项目运行maven->update project命令时报错:org/apache/maven/shared/filtering/MavenFiltering ...

  8. Nutch学习笔记二——抓取过程简析

    在上篇学习笔记中http://www.cnblogs.com/huligong1234/p/3464371.html 主要记录Nutch安装及简单运行的过程. 笔记中 通过配置抓取地址http://b ...

  9. 百科知识 isz文件如何打开

    使用UltraISO可以打开

  10. Codeforces Beta Round #1 A. Theatre Square

    从今天開始.就要在Codeforces里有一个新的開始了,貌似任务非常重的说~~ Codeforces专题我将会记录全部通过的题目,事实上仅仅要通过的题目都是水题啊!. 题目大意: 依照要求计算须要多 ...