「LuoguP3376」 【模板】网络最大流

题目描述

如题，给出一个网络图，以及其源点和汇点，求出其网络最大流。

输入输出格式

输入格式：

第一行包含四个正整数N、M、S、T，分别表示点的个数、有向边的个数、源点序号、汇点序号。

接下来M行每行包含三个正整数ui、vi、wi，表示第i条有向边从ui出发，到达vi，边权为wi（即该边最大流量为wi）

输出格式：

一行，包含一个正整数，即为该网络的最大流。

输入输出样例

输入样例#1：
复制

4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 40

输出样例#1： 复制

50

说明

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=10，M<=25

对于70%的数据：N<=200，M<=1000

对于100%的数据：N<=10000，M<=100000

样例说明：

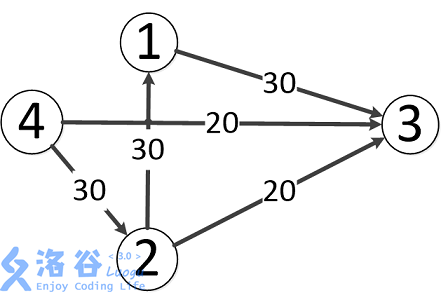
题目中存在3条路径：

4-->2-->3，该路线可通过20的流量

4-->3，可通过20的流量

4-->2-->1-->3，可通过10的流量（边4-->2之前已经耗费了20的流量）

故流量总计20+20+10=50。输出50。

---

题解

就是个模板题啊！QAQ

//其实就是挂个板子2333

 /*
     qwerta
     P3376 【模板】网络最大流
     Accepted
     100
     代码 C++，1.68KB
     提交时间 2018-07-12 17:31:29
     耗时/内存
     140ms, 4847KB
 */
 #include<cmath>
 #include<queue>
 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;
 struct emm{
     int e,f,v;
 }a[];//邻接链表存边
 int h[],cur[];//cur:当前弧优化（没什么用
 int n,m,s,t;
 int tot=;
 inline int read()//快读
 {
     char ch=getchar();
     int s=,x=;
     while(ch<''||ch>''){if(ch=='-')s=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-;ch=getchar();}
     return s*x;
 }
 inline void con(int l,int r,int w)//加边
 {
     a[++tot].f=h[l];
     h[l]=tot;
     //cur[l]=h[l];
     a[tot].e=r;
     a[tot].v=w;
     return;
 }
 inline void scan()//读入，建图
 {
     n=read(),m=read(),s=read(),t=read();
     for(int i=;i<=m;++i)
     {
         int z=read(),y=read(),l=read();
         con(z,y,l);
         con(y,z,);
     }
     return;
 }
 //Dinic
 queue<int>q;//bfs的queue
 int  d[];//分层图的深度
 inline bool bfs()
 {
     memset(d,,sizeof(d));//初始化
     d[s]=;//标记源点深度
     q.push(s);
     for(int i=;i<=n;++i)cur[i]=h[i];//恢复cur数组
     while(!q.empty())
     {
         int now=q.front();
         q.pop();
         //扩张
         for(int i=h[now];i;i=a[i].f)
         if(!d[a[i].e]&&a[i].v)//若未被标记过并且该边在残量网络中
         {
             d[a[i].e]=d[now]+;
             q.push(a[i].e);
         }
     }
     return d[t];//返回s,t是否联通
 }
 int dfs(int x,int al)
 {
     if(x==t||!al)return al;
     int tot=;
     for(int i=cur[x];i;i=a[i].f)
     {
         cur[x]=i;//当前弧优化
         if(d[a[i].e]==d[x]+&&a[i].v)
         {
             int f=dfs(a[i].e,min(al,a[i].v));//往下找
             if(f)//若非0
             {
                 a[i].v-=f;
                 a[i^].v+=f;
                 tot+=f;
                 al-=f;
                 if(!al)break;
             }
         }
     }
     if(!tot)d[x]=-;//最有用的优化！（敲黑板
     return tot;//返回流量值
 }
 inline void run()//运行
 {
     long long ans=;
     while(bfs())ans+=dfs(s,);
     cout<<ans;
     return;
 }
 int main()//超短主函数（当年码风真奇怪orz
 {
     scan();
     run();
     return ;
 }