运用模逆运算(同余方程)来解决Matlab课上的一道思考题
一个篮子有K个鸡蛋:
2个2个拿剩1个;
3个3个全部拿完;
4个4个拿剩1;
5个5个拿剩4个;
6个6个拿剩3个;
7个7个拿全部拿完;
8个8个拿剩1个;
9个9个拿全部拿完;
求篮子里鸡蛋的个数K
虽然这是一道matlab拿来玩的题目,可是我觉得完全可以拿来做笔试题或者面试题。仔细想还是有点考算法能力的。
resultNum = [];
resultIndex = 0;
i = 1;
while 63*i < 1000000000
while 1
i = i + 2;
if max(abs(rem(63*i, inputDivisors) - modResult)) == 0
break
end
end
resultNum(resultIndex + 1) = 63*i;
resultIndex = resultIndex +1;
end
disp(resultIndex)
resultNum( resultIndex)
我们先来看下枚举本身为什么会慢的问题,我们可以看到,枚举每一次都要尝试和M个除数进行相除,然后得到余数,除了本身求余这种对CPU的ALU指令非常不友好导致速度有瓶颈以外,还有最致命的就是枚举要通过不断地 “试验” 来得到判断的目的,当然这个过程可以裁枝(就像上面所说的观察法),但是这个问题的裁枝也只是减少了复杂度MN前面的常数系数。
step1: 63k
step2: 63*(2k + i)
step3: 63*(2(2k + j) + i) = 63*(4k + 2j + i)
step4: 63*(4(5k + l) + 2j + i) = 63*(20k + 4l + 2j + i)
step5: 63*(20(k + m) + 20l + 2j + i) = 63*(20k + 20m + 4l + 2j + i)
step6: 63*(20(2k + n) + 20m + 4l + 2j + i) = 63*(40k + 20n + 20m + 4l + 2j + i)
设存在方程 ax + by = L如果该方程的线性同余形式为 ax = L mod b如果这个形式下该方程有解,那么L一定且仅满足gcd(a,b) == L时成立
定理一:如果d = gcd(a, b),则必能找到正的或负的整数k和l,使d = ax+ by。定理二:若gcd(a, b) = 1,则方程ax ≡ c (mod b)在[0, b-1]上有唯一解。定理三:若gcd(a, b) = d,则方程ax ≡ c (mod b)在[0, b/d - 1]上有唯一解。
%External Euclidean Algorithm
%xPtr is a pointer, x is p(1), y is p(2)
%warnning: the index is different from C\C++
function result = ExMyGcd(n,m, xPtr)
if n == 0
find= m;
xPtr.value(1) = 1;
xPtr.value(2) = 0;
else
num=[0,0];
numPtr=libpointer('int32Ptr', num);
find = ExMyGcd(rem(m,n), n, numPtr); xPtr.value(1) = numPtr.value(2);
xPtr.value(2) = numPtr.value(1) - numPtr.value(2)*floor(m/n);
end
result = find;
end %ExMyGcd
obj = SearchPolyFuntionHelper(inputDivisors, modResult, 1, 1, 0);
obj = DoSearch(obj);
n = 0;
if obj.m_isValid == 0
disp('invalid condition') %不满足同余定理的条件,直接舍弃
else
coefficient = obj.m_coefficient;
innerCofficient = obj.m_innerCofficient;
offset = obj.m_offset; resultNum = [];
resultIndex = 0;
while 1
r = coefficient *(innerCofficient * n + offset);
if (r >=1000000000)
break
end
resultNum(resultIndex + 1) = r;
resultIndex = resultIndex + 1;
n = n + 1;
end
disp(resultIndex)
resultNum( resultIndex)
end
classdef SearchPolyFuntionHelper
methods (Access = 'public')
function obj = SearchPolyFuntionHelper(divisors, modResult, coefficient, innerCofficient, offset)
obj.m_divisors = divisors;
obj.m_modResult = modResult;
obj.m_coefficient = coefficient;
obj.m_innerCofficient = innerCofficient;
obj.m_offset = offset;
obj.m_isValid = 1; end % SerchPolyFuntionHelper function obj = DoSearch(obj)
sum = size(obj.m_divisors);
for n = 1: sum(2)
if obj.m_modResult(n) == 0
mCoefficient = obj.m_coefficient;
mDivisors = obj.m_divisors(n);
gcdDivisor = gcd(mCoefficient, mDivisors);
if gcdDivisor ~= mDivisors
obj.m_coefficient = mCoefficient*mDivisors / gcdDivisor;
end
end
n = n + 1;
end
for n = 1: sum(2)
if obj.m_modResult(n) ~= 0
obj = Expand(obj, n); if obj.m_isValid ==0
return
end
end
n = n + 1;
end
end %DoSearch
end
methods(Access = 'private')
%Expand the cofficent
function dObj =Expand(dObj, index)
%先确定最小公倍数
mDivisors = dObj.m_divisors(index);
gcdDivisor = gcd(dObj.m_coefficient * dObj.m_innerCofficient, mDivisors); oldInnerCofficient = dObj.m_innerCofficient;
dObj.m_innerCofficient = oldInnerCofficient * mDivisors / gcdDivisor; %确定偏移量 coefficient*oldInnerCofficient*i + offset ( i>=0)
mod = dObj.m_modResult(index);
offset = dObj.m_offset; offsetMod = rem(offset * dObj.m_coefficient, mDivisors); %得到偏移量的余数
lastMod = rem(mod - offsetMod + mDivisors, mDivisors); if lastMod ~=0 %如果当前offset已经可以满足余数,就不需要再加了
num=[0,0];
xPtr=libpointer('int32Ptr',num);
mul = dObj.m_coefficient* oldInnerCofficient;
gcdDivisor = ExMyGcd(mDivisors, mul, xPtr); if rem(lastMod, gcdDivisor) ~=0
dObj.m_isValid = 0; %如果不满足同余定理,说明无法找到这样的多项式,直接退出
return;
end newCofficient= xPtr.value(1);
newCofficient = newCofficient * lastMod/ gcdDivisor;
dObj.m_offset = newCofficient* oldInnerCofficient + offset;
end
end%Expand
end
properties (Access = 'public')
m_coefficient;
m_innerCofficient;
m_offset;
m_divisors;
m_modResult;
m_isValid;
ElementIndex;
end
properties (Dependent)
Modulus
end
end
%External Euclidean Algorithm
%xPtr is a pointer, x is p(1), y is p(2)
%warnning: the index is different from C\C++
function result = ExMyGcd(n,m, xPtr)
if n == 0
find= m;
xPtr.value(1) = 1;
xPtr.value(2) = 0;
else
num=[0,0];
numPtr=libpointer('int32Ptr', num);
find = ExMyGcd(rem(m,n), n, numPtr); xPtr.value(1) = numPtr.value(2);
xPtr.value(2) = numPtr.value(1) - numPtr.value(2)*floor(m/n);
end
result = find;
end %ExMyGcd
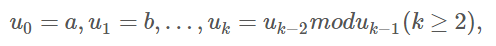
 我们比较数列{un}和菲波那契数列{Fn},
我们比较数列{un}和菲波那契数列{Fn},
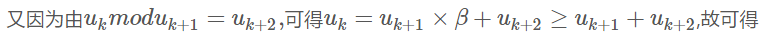


也就是
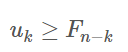
 ,也就是说如果欧几里得算法需要做n次模运算, 则b必定不小于Fn−1. 根据斐波那契数列的性质, 有
,也就是说如果欧几里得算法需要做n次模运算, 则b必定不小于Fn−1. 根据斐波那契数列的性质, 有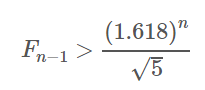
 ,所以模运算的次数为O(lgb)
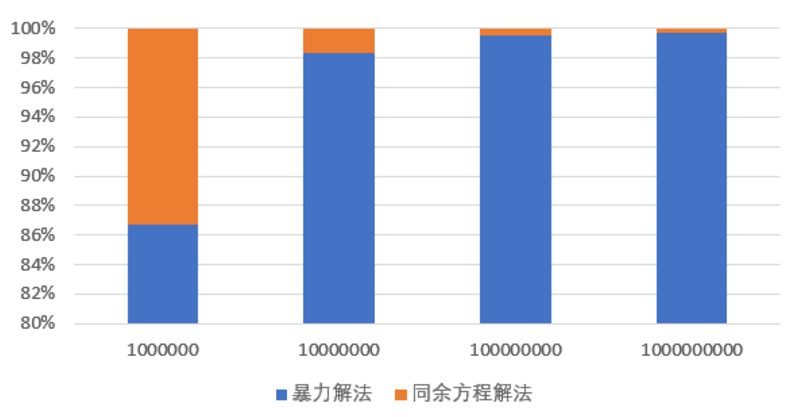
,所以模运算的次数为O(lgb)暴力算法与用同余方程的算法在需要算出n以内鸡蛋数的条件下,进行时间复杂度的比较结果。
clear
clc
mainFun()
function mainFun()
modResult = [1,0,1,4,3,0,1,0];
inputDivisors = [2:9]; disp('-----------------Mytest-----------------')
tic;
obj = SearchPolyFuntionHelper(inputDivisors, modResult, 1, 1, 0);
obj = DoSearch(obj);
n = 0;
if obj.m_isValid == 0
disp('invalid condition') %不满足同余定理的条件,直接舍弃
else
coefficient = obj.m_coefficient;
innerCofficient = obj.m_innerCofficient;
offset = obj.m_offset; resultNum = [];
resultIndex = 0;
while 1
r = coefficient *(innerCofficient * n + offset);
if (r >=1000000000)
break
end
resultNum(resultIndex + 1) = r;
resultIndex = resultIndex + 1;
n = n + 1;
end
disp(resultIndex)
resultNum( resultIndex)
end toc;
vpa(tic - toc); disp('-----------------OridnaryTest-----------------')
tic;
resultNum = [];
resultIndex = 0;
i = 1;
while 63*i < 1000000000
while 1
i = i + 2;
if max(abs(rem(63*i, inputDivisors) - modResult)) == 0
break
end
end
resultNum(resultIndex + 1) = 63*i;
resultIndex = resultIndex +1;
end
disp(resultIndex)
resultNum( resultIndex)
toc;
vpa(tic - toc);
end
运用模逆运算(同余方程)来解决Matlab课上的一道思考题的更多相关文章
- 如何解决 Matlab 画图时中文显示乱码的问题?
使用的是win10系统,从前几个月某一天,我的matlab的figure里的中文都变成了口口.很是郁闷,还以为是动到了什么配置引起的. 前几天更新了matlab 2018b,发现还有这个问题.就觉得不 ...
- 20165223《信息安全系统设计基础》第九周学习总结 & 第八周课上测试
目录 [第九周学习总结] 教材内容总结 [第八周课上测试] (一)求命令行传入整数参数的和 (二)练习Y86-64模拟器汇编 (三)基于socket实现daytime(13)服务器和客户端 参考资料 ...
- 20175316盛茂淞 2018-2019-2 《Java程序设计》第2周课上测试总结
20175316 2018-2019-2 <Java程序设计>第2周课上测试总结 上周考试题目总结 题目1 题目要求: 在Ubuntu中用自己的有位学号建一个文件,教材p29 Exampl ...
- 20165305 苏振龙《Java程序设计》第四周课上测试补做
第一次测试 第二次测试 第三次测试 上传代码 第四次测试 总结 之前我一直在git bash进行程序设计,但是对于我来说操作起来有点困难,所以我改用了虚拟机,之后之前一直困扰我的问题在虚拟机下就没有了 ...
- # 2017-2018-1 20155302 课下实践IPC及课上补充
课上实践补交 题目二要求: 学习使用stat(1),并用C语言实现 提交学习stat(1)的截图 man -k ,grep -r的使用 伪代码 产品代码 mystate.c,提交码云链接 测试代码,m ...
- 2017-2018-1 20155232 《信息安全系统设计基础》第四周学习总结以及课上myod练习补充博客
2017-2018-1 20155232 <信息安全系统设计基础>第四周学习总结以及课上myod练习补充博客 课上myod练习 1 参考教材第十章内容 2 用Linux IO相关系统调用编 ...
- 2018-2019-1 20165330 《信息安全系统设计基础》第六周课上测试ch02&课下作业
课上测试 测试-3-ch02 任务详情 编写一个程序 "week0203学号.c",运行下面代码: 1 short int v = -学号后四位 2 unsigned short ...
- Java实验--关于课上找“水王”问题分析
问题的表述就是说有那么一个人,他在一个论坛上发帖,然后每贴必回,自己也发帖.那么这个人在发帖的数目上就超过了整个论坛的帖子数目的一半以上. 我对这个问题一开始的思路是,用SQL语句获取整个列表中的数据 ...
- 关于转入软件工程专业后第二次java课上作业的某些体会
今天是第二周的java课. 自从转入了软件工程专业后,在我没有学习c++的基础上,直接开始了学习java的过程.不得不说过程很艰辛.今天下午老师让编写一个随机产生作业的软件.而我的基础差到都不知道如何 ...
随机推荐
- HDU3478 【判奇环/二分图的性质】
题意: 给你一幅图,给你一个起点,然后问你存不存在一个时刻,所有点可以在那个时刻到达. 思路: 这幅图首先是联通的: 如果出现奇数环,则满足在某一时刻都可能到达: 然后判断奇数环用二分图性质搞也是神奇 ...
- Unity3d的批渲染 batch rendering
http://blog.csdn.net/leonwei/article/details/41942157 批渲染(Batch) batch render 是大部分引擎提高渲染效率的方法,基本原理就是 ...
- git clone 之后 , 如何复制文件到文件夹 并 上传
1. 关于 _netrc machine github.com login myid password mypassword machine bitbucket.org login myid pass ...
- Mol Cell Proteomics. |廖文丽| 阿尔兹海默症临床前期的脑脊液中突触蛋白的变化先于神经变性标志物
大家好,本周分享的是发表在Molecular & Cellular Proteomics. 上的一篇关于阿尔兹海默病临床前期生物标志物鉴定的文章,题目是Changes in synaptic ...
- javaScript中for-in语句
for-in语句是一种精准的迭代语句,用来枚举对象的属性 实例: <!DOCTYPE html><html><head> <title>For-In S ...
- load View 流程 程序启动流程
基本流程: loadView / nib文件 来加载view到内存 -> viewDidLoad 函数进一步初始化这些view -> 内存不足时, 调用viewDidUnload 函数释 ...
- 解决DDOS攻击生产案例
根据web日志或者或者网络连接数,监控当某个IP并发连接数或者短时内PV达到100,即调用防火墙命令封掉对应的IP. 当然各个公司的IP并发数各有不同,上面只是举例说明. 因为我的Nginx的WEB日 ...
- B. Mancala (Codeforces Round #478 (Div. 2))
#include <bits/stdc++.h> using namespace std; ; typedef long long ll; ll a[maxn]; ll b[maxn]; ...
- iOS开发 - RunLoop理解
RunLoop概念 运行循环,一个 run loop 就是一个事件处理的循环,用来不停的调度工作以及处理事件 作用 保持程序的持续运行 监听处理App中的各种事件(触摸事件,定时器事件,selecto ...
- php—常见设计模式
工厂模式 /** * 工厂方法或者类生成对象,而不是在代码中直接new * * 修改类名的时候,不需要每一个实例化语句都修改 * 只需要修改对应的工厂方法 * * Class Factory * @p ...
